Dirichlet Process Mixture Model
Nội dung bài viết
Dirichlet Process Mixture Model (DPMM) là một thuật toán phân cụm nằm trong nhóm thống kê phi tham số Bayesian, sỡ dĩ gọi là phi tham số vì bạn không cần phải thiết lập tham số (nhưng không có nghĩa là mô hình không có tham số). Mô hình này được ứng dụng nhiều vào trong các bài toán phân cụm khi chưa biết trước số cụm, đôi lúc dùng để xấp xĩ hàm mật độ,…
Dirichlet Process Mixture Model (DPMM) có nhiều ứng dụng thực tiễn, đặc biệt trong bài toán phân tích cụm khi chưa biết số cụm (khi mà lượng dữ liệu lớn và số chiều cao). Dẫu có rất nhiều phương pháp được thiết kế để “đoán số cụm” của dữ liệu, song phần lớn hướng tiếp cận chủ yếu được xây dựng như là một “mẹo giải” (heuristic), phương pháp này khá đặc biệt vì hướng tiếp cận được xây dựng chặt chẽ từ mô hình lý thuyết.
Mô hình vô hạn của Dirichlet Process Mixture Model khởi tạo một lượng lớn số cụm không cần thiết và sử dụng chúng để thoát khỏi cục bộ địa phương. Hãy cùng nhau khám phá thuật toán này nhé!
1. Bài toán quá trình nhà hàng Trung Hoa
Chinese Restaurant Process
Trước khi đến với bài toán gốc, chúng ta hãy cùng nhau khảo sát bài toán “quá trình nhà hàng trung hoa” vì nó có liên hệ đến ý tưởng mô hình hóa của mô hình “vô số cụm” trong bài toán sắp tới.
Tưởng tượng một nhà hàng kỳ lạ:
- Nhà hàng có vô hạn chiếc bàn.
- Mỗi chiếc bàn có thể chứa vô hạn khách.
Mỗi khách đến với nhà hàng và ngồi vào một cái bàn với cơ hội:
- Ngồi vào một bàn $c$ đang có người ngồi: $$p(\text{ngồi ở bàn } c) = \frac{n_c}{\alpha + \sum_{c} n_c}$$
- Ngồi vào một bàn mới chưa có người ngồi: $$p(\text{ngồi ở bàn } \textbf{mới}) = \frac{\alpha}{\alpha + \sum_{c} n_c}$$
Với $\alpha$ được là một tham số tỉ lệ (còn gọi là “độ tập trung”), $\alpha$ càng lớn thì có vẻ như rằng nhà hàng phải mở nhiều bàn hơn, $\alpha$ càng nhỏ thì có vẻ nhà hàng mở với số lượng bàn ít hơn, $n_c$ là số lượng người hiện tại đang ngồi ở bàn $c$, do đó $\sum_{c}$ là số khách hàng đang ngồi tại nhà hàng Trung Hoa.
Quá trình trên được gọi là “quá trình nhà hàng Trung Hoa được định nghĩa bởi [Aldous 1985, Pitman 2006].
Bài toán này thật sự không có gì đặc biệt, nếu như chúng không thử mô phỏng nó tí xem.
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: Python 3.7.3 (Anaconda) | |
# | > Mô phỏng bài toán nhà hàng trung hoa | |
# |_____________________________________________________________________|/
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from matplotlib import style
style.use('fivethirtyeight')
# gán seed để máy bạn và máy mình ra cùng kết quả
np.random.seed(0)
def chinese_restaurant_process(alpha, n):
"""
Mô phỏng bài toán nhà hàng trung hoa
:param alpha: hệ số alpha của bài toán CRP
:param n: số lượng khách hàng
:return count: số lượng bàn được mở
"""
i = 0
# với mỗi table[k] là số người đang ngồi ở bàn k
table = []
for i in range(n):
prob = list(map(lambda x: x/(alpha + i), table))
prob.append(alpha/(alpha + i))
# chuẩn hóa prob để dùng stats.rv_discrete
# tránh sai số do số thực
prob = np.array(prob)
prob = prob / prob.sum()
# label cuối là -1 (quy ước là mở bàn mới)
label = list(range(len(table)))
label.append(-1)
# lấy con số đại diện bàn cho khách hàng
current_dist = stats.rv_discrete(name='dist', values=(label, prob))
pos = int(current_dist.rvs(size=1))
if pos == -1:
# Nếu mở bàn mới thêm một bàn mới với số lượng 1 người
table.append(1)
else:
# Nếu ngồi bàn cũ thì vị trí đó thêm một người
table[pos] += 1
# đếm số lượng bàn
count = len(table)
return count
def simulate_crp(alpha, step, max_iter, n_simulate):
"""
Giả lập bài toán nhà hàng Trung Hoa
:param alpha: hệ số alpha
:param step: mỗi vòng lặp tăng step khách hàng
:param max_iter: số lượng vòng lặp
:return list_n_table: với list_n_table[k] chứa n_simulate giả lập
với alpha và step*k
"""
list_n_table = []
for i in range(1, max_iter+1):
print('Iter: %d' % i)
n_table = []
for _ in range(n_simulate):
n_table.append(chinese_restaurant_process(alpha, i*step))
list_n_table.append(n_table)
return list_n_table# mô phỏng
list_n_table = simulate_crp(30, 50, 50, 100)
for i in range(50):
x = [i+1] * 100
plt.scatter(x, list_n_table[i], color = '#007aff', s = 1.2)
x_mean = []
y_mean = []
for i in range(50):
x_mean.append(i+1)
y_mean.append(sum(list_n_table[i]) / 100.0)
plt.plot(x_mean, y_mean, color='#ff2d55')
plt.xlabel('Số lượng khách hàng')
plt.ylabel('Số lượng bàn')
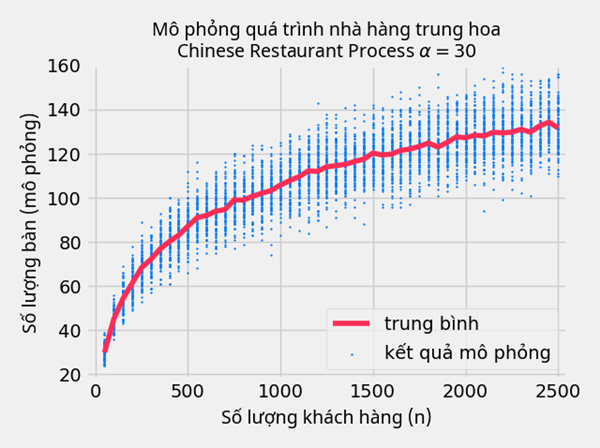
plt.show()Liệu bạn có cảm giác rằng số lượng bàn tăng theo hàm logarít không?
Đặt $q$ là biến ngẫu nhiên số bàn cần phải trang bị khi biết hệ số $\alpha$ và $n$ khách hàng tới nhà hàng, những nhà toán học xấp xĩ được kỳ vọng và phương sai của $q$ của nhà hàng kỳ lạ này:
- Kỳ vọng: $$\mathbb{E} \left[ q | \alpha, n \right] \approx \alpha \ln{\left(1+\frac{n}{\alpha} \right)} $$
- Phương sai: $$\mathbb{V} \left[ q | \alpha, n \right] \approx \alpha \ln{\left(1+\frac{n}{\alpha} \right)} $$
Thử vẽ hình ra xem liệu công thức trên có đúng không nào!
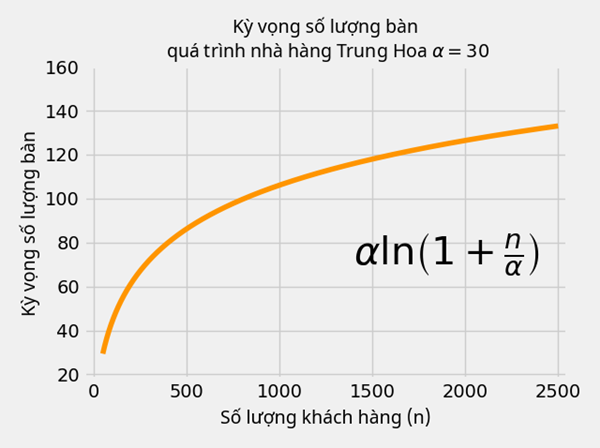
Liệu việc tăng số bàn khá chậm theo hàm logarít này có dẫn đến điều gì đặc biệt không?
Hãy cùng nhau đi làm bồi bàn vài bữa ở “Nhà hàng Trung Hoa” để hiểu quá trình trong nhà hàng này cùng phép ẩn dụ “khách là điểm” còn “bàn là cụm”… Thật lạ, ông chủ cứ bảo “bàn thì anh không thiếu (nhà hàng kỳ quặc vô hạn bàn) mà nhiều thì anh không có (thực tế chỉ hữu hạn dao động trong nhường dăm ba cái là cùng)“… thật kỳ quặc mà, hãy chờ xem…
2. Dirichlet Process
Quá trình Dirichlet (Dirichlet Process) là một quá trình ngẫu nhiên thường được sử dụng trong các mô hình thống kê phi tham số Bayesian. Dirichlet Process được định nghĩa bởi [Ferguson 1973] như là một phân bố trên một phân bố khác (tạm gọi là “phân bố nền” - base distribution). Nó là một trong những nền tảng quan trọng của một số mô hình thống kê phi tham số Bayesian.
Dirichlet Process xác định bởi hai tham số là phân bố nền $H$ và một số dương $\alpha$ được gọi là độ tập trung. Gọi $G$ là một biến ngẫu nhiên có phân bố Dirichlet Process cho phân bố $H$ cùng hệ số $\alpha$ ta có thể viết:
$$ G \sim \text{DP}(\alpha, H)$$
Lúc này với mỗi một tập hữu hạn phần tử phân hoạch không gian xác suất $A_1,…, A_r$, vectơ ngẫu nhiên $(G(A_1),…,G(A_r))$ được phân bố ngẫu nhiên theo $G$, ta gọi biến ngẫu nhiên $G$ được phân bố theo Dirichlet Process với phân bố nền $H$ cùng độ tập trung $\alpha$ hay $G \sim \text{DP}(\alpha, H)$ nếu vectơ ngẫu nhiên này thỏa:
$$ G(A_1),…,G(A_r)) \sim \text{Dir}(\alpha H(A_1), …, \alpha H(A_r))$$
Trong đó $\text{Dir}$ là phân bố Dirichlet (tập các trường hợp xảy ra của phân bố này thỏa mỗi vectơ có tổng bằng $1$ nằm trong một đơn hình (hay còn gọi là simplex), hàm mật độ cần tham số của một vectơ hệ số dương).
Dirichlet Process có nhiều cách để xây dựng một quá trình xác suất để thỏa mãn những yêu cầu trên. Hai phép “ẩn dụ” phổ biến nhất của quá Dirichlet Process mà bạn đọc nên quan tâm là:
- Chinese restaurant process.
- Stick-breaking construction.
Phần này chúng ta sẽ không phân tích chi tiết ở đây.
Ngay bây giờ, chúng ta sẽ tìm hiểu Dirichlet Process một cách trực cảm! Chúng ta sẽ tìm hiểu Dirichlet Process theo sự thay đổi tham số $H$ và $\alpha$ để hiểu “đôi phần về quá trình này”!
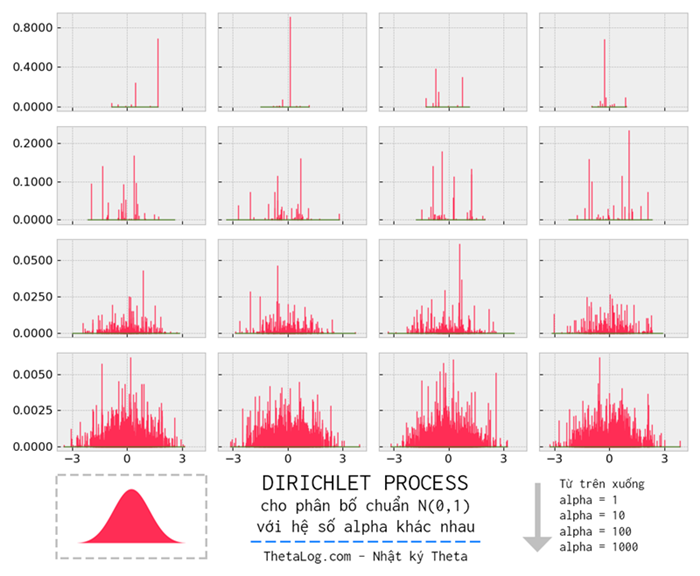
Hình trên là Dirichlet Process với tham số phân bố $H$ là phân bố chuẩn $\mathcal{N}(0,1)$ với hệ số $\alpha$ thay đổi từ trên xuống $1, 10, 100, 1000$ khi lấy $1500$ mẫu, nhận xét:
- Dirichlet Process làm “rời rạc hóa” phân bố nền, $H$ có thể là một phân bố liên tục và trơn, tuy nhiên phân bố $\text{DP}(\alpha, H)$ thì lại rời rạc, không trơn hơn phân bố nền.
- Khi tham số $\alpha$ (độ tập trung) tiến về $0$ hay $\alpha \rightarrow 0$, phân bố Dirichlet Process càng “rời rạc”, tập trung tại một vài trường hợp có thể xảy ra của phân bố $H$.
- Khi tham số $\alpha$ (độ tập trung) tiến về $\infty$ hay $\alpha \rightarrow \infty$, phân bố Dirichlet Process càng “liên tục”, ít tập trung hơn tại một vài trường hợp có thể xảy ra phân bố $H$ hơn, giá trị $\alpha$ càng cao thì phân bố Dirichlet Process càng giống phân bố $H$.
3. Mô hình sinh dữ liệu của mô hình trộn theo cách nhìn từ Dirichlet Process
Trong phần này chúng ta sẽ thảo luận về mô hình sinh dữ liệu của mô hình trộn (Mixture Model) theo cách nhìn từ Dirichlet Process.
Trong xác suất thống kê, một mô hình trộn là một mô hình xác suất để biểu diễn cho mô hình tổng thể bằng sự hiện diện của các phân bố con theo hệ số trộn. Hay nói cách khác, một phân bố tổng quát có thể biểu diễn bằng việc trộn của các phân bố con, giả sử có $K$ phân bố con, mỗi phân bố con thứ $k$ được cho bởi một tham số $\theta_i$:
$$p(x | \theta) = \sum_{k=1}^K \pi_k p_k(x | \theta_k)$$
Ví dụ, mô hình trộn của phân bố chuẩn được xác định bởi tham số kỳ vọng $\mu$ và ma trận hiệp phương sai $\Sigma$, ta có thể viết lại:
$$p(x | \theta) = \sum_{k=1}^K \pi_k \mathcal{N}(x | \mu_k, \Sigma_k)$$
Giả sử mỗi tham số $\theta_k$ được sinh ra từ một phân bố $H$ nào đó.
Hãy nghĩ về một quá trình Dirichlet Process nọ cho phân bố $H$ và tham số $\alpha$ sinh ra các bộ tham số $\bar{\theta_i}$ nào đó $N$ lần, mỗi tham số $\bar{\theta_i}$ này sẽ dùng để sinh ra các điểm dữ liệu $x_i$.
Như ta đã biết, Dirichlet Process sẽ làm rời rạc hóa phân bố gốc và tạo một phân bố mới tập trung tại một số giá trị phân bố $H$.
Tập các bộ tham số $\{\bar{\theta_1}, …, \bar{\theta_N} \}$ có những bộ tham số được lặp đi lặp lại nhiều lần! Giả sử tập bộ tham số được lặp đi lặp lại gồm có $K$ bộ tham số khác nhau $\bar{\theta_i} \in \{ \theta_1, …, \theta_K \}$, chúng ta có thể hình dung quá trình này sinh ra một tập dữ liệu có mô hình trộn $K$ cụm.
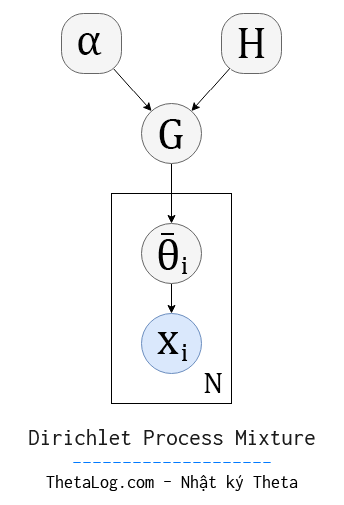
4. Dirichlet Process Mixture Model
Dirichlet Process Mixture Model là mô hình mà giả thuyết là phân bố trộn của dữ liệu được sinh ra được xem như là một quá trình Dirichlet bởi một phân bố tham số của $\theta$.
Mô hình Bayesian này có nhiều cách để tìm tham số. Một trong những cách thông dụng nhất là dùng kỹ thuật MCMC (Markov Chain Monte Carlo) hoặc dùng kỹ thuật biến phân (Variantional Inference).
Mỗi một cách định nghĩa mô hình đồ thị khác nhau sẽ dẫn đến chúng ta có cách giải quyết bài toán khác nhau. Định nghĩa mô hình đồ thị như phần 3 chúng ta vẫn có thể giải quyết bài toán. Tuy nhiên mô hình trên không hiệu quả cho bài toán này, bạn đọc có thể tham khảo 8 thuật toán MCMC của Radford M. Neal, mô hình đồ thị như phần 3 chính là thuật toán thứ 1 trong bài báo “Markov Chain Sampling Methods for Dirichlet Process Mixture Models”.
Với mô hình trộn $K$ cụm sinh $N$ điểm dữ liệu $x_i$, mỗi điểm dữ liệu gán nhãn thuộc về cụm $z_i$ chúng ta có thể biểu diễn mô hình trộn hữu hạn Bayesian như sau (đã gắn tiên nghiệm cho các tham số cần thiết):
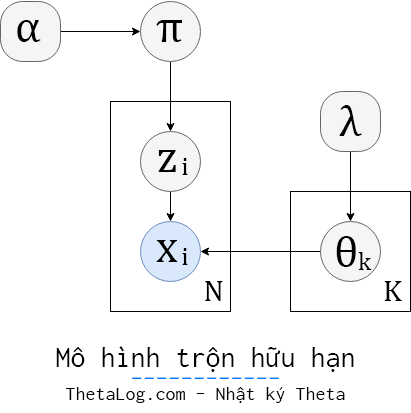
Với mô hình trên, khi biết điểm dữ liệu $x_i$ thuộc về cụm $k$ và có tập tham số $\theta$ ta có:
$$ p(x_i | z_i = k, \theta) = p(x_i | \theta_k)$$
Gọi $\pi$ là một vectơ $k$ thành phần có tổng là $1$ thể hiện hệ số trộn của mô hình trộn, lúc này xác suất dữ liệu thuộc về cụm $k$ tương ứng là:
$$p(z_i = k | \pi) = \pi_k$$
Xem $\pi$ được sinh ra từ phân bố Dirichlet với tham số $\alpha$ (ký hiệu $\text{1}_K$ thể hiện một vectơ $K$ thành phần đều là $1$):
$$p(\pi | \alpha) = \text{Dir}(\pi | (\alpha/K) \text{1}_K)$$
Mỗi tham số $\theta_k$ được sinh ra từ một phân bố $\theta_k \sim H(\lambda)$, để thuận lợi cho việc tính toán phân bố tiên nghiệm $p(\theta_k | \lambda)$ sẽ được chọn liên hợp với phân bố $p(x_i | \theta_k)$. (từ thuật toán 1 đến 3 trong bài báo của Radford M. Neal là trường hợp dùng tiên nghiệm liên hợp, từ thuật toán số 4 trở về sau dùng cho trường hợp không sử dụng tiên nghiệm liên hợp).
Lúc này khi biết $x_i$ thuộc cụm $\theta_k$, ta có thể viết $p(x_i | \theta_k)$ được sinh ra từ phân bố $x_i \sim F(\theta_{z_i})$ với $F$ là phân bố con được dùng trong mô hình trộn.
Nhờ tính có thể “hoán đổi” được (exchangeable random variables) trong trường hợp bài toán này, và giả sử rằng phân bố $H$ thì liên hợp với $F$, chúng ta có thể sử dụng Collapsed Gibbs Sampling (lược bỏ đi $\pi$ và $\theta_k$) trong mô hình, việc chúng ta cần tìm bây giờ là đi tìm $z_i$.
Loại $\pi$ và $\theta_k$ ra khỏi công thức Gibbs Sampling, phân bố có điều kiện của $z$ khi biết trước tập dữ liệu $x$ cùng với cụm của các điểm dữ liệu khác tỉ lệ với:
$$\color{purple} p(z_i = k | \mathbf{z}_{-i}, \mathbf{x}, \alpha, \lambda) \color{black} \propto \color{red} p(z_i = k | \mathbf{z}_{-i}, \alpha) \color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k, \lambda)$$
(từ phần này về hai phần sau $n_{k, -i}$ là số lượng điểm thuộc cụm $k$ ngoại trừ điểm $x_i$)
Bởi tính có thể “hoán đổi” được, giả sử $z_i$ là điểm dữ liệu cuối cùng được tạo ra (hay “khách hàng đến nhà hàng cuối cùng” trong phép ẩn dụ bài toán nhà hàng Trung Hoa) mà công thức $\color{red} p(z_i = k | \mathbf{z}_{-i}, \alpha)$ trở nên “dể chịu” hơn rất nhiều.
Vì sao cần phải sử dụng tiên nghiệm liên hợp (conjugate prior) trong bài toán này? Hãy quan sát công thức màu xanh $ \color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k, \lambda)$ đây là một công thức “khó tính” trong nhiều trường hợp!
4.1 (hữu hạn) Trường hợp cho biết trước số cụm
Trong trường hợp biết trước số cụm $K$, ta có:
$$\color{red} p(z_i = k | \mathbf{z}_{-i}, \alpha) \color{black} = \frac{ n_{k, -i} + \frac{\alpha}{K} }{\alpha + N - 1}$$
Và:
$$ \color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k, \lambda) \color{black} \propto \int p(x_i | \theta_k) \left[ \prod_{j \neq i, z_j = k} p(x_j | \theta_k) \right] H(\theta_k | \lambda) d \theta_k$$
Mã giả thuật toán:
$\mathtt{clusters} \leftarrow$ tạo $K$ cụm, mỗi cụm là một phân bố (cùng tiên nghiệm liên hợp tương ứng)
For $\mathtt{i}$ trong $1$ đến $N$ lặp: {
$z_i \leftarrow $lấy ngẫu nhiên thuộc từ $1$ đến $K$
Thêm $x_i$ vào cụm $\mathtt{clusters}[ z_i ]$, cập nhật các tham số cần thiết
}
For $\mathtt{iter}$ trong $1$ đến $\mathtt{maxiter}$ lặp: {
For $\mathtt{i}$ trong $1$ đến $N$ lặp: {
Xóa $x_i$ trong cụm $\mathtt{clusters}[ z_i ]$, cập nhật các tham số cần thiết
Tính và chuẩn hóa $\color{purple} p(z_i | \mathbf{z}_{-i}, \mathbf{x}, \alpha, \lambda)$, gọi phân bố rời rạc này là $p(z_{\mathtt{new}} | .)$
Lấy mẫu $z_{\mathtt{new}} \sim p(z_{\mathtt{new}} | .)$
Thêm $x_i$ vào cụm $\mathtt{clusters}[ z_{\mathtt{new}} ]$, cập nhật các tham số cần thiết
}
}
RETURN $z$
4.2 (vô hạn) Trường hợp chưa biết trước số cụm
Trong phần này chúng ta kí hiệu $k^{*}$ là cụm mới và $\theta^{*}$ là tham số cụm mới, $k$ là cụm cũ và $\theta_k$ là tham số cụm cũ.
Trong trường hợp chưa biết số cụm, giả sử khởi tạo có $K$ cụm, tại mỗi lần chúng ta cho phép điểm đó nhảy sang các cụm hiện có, hoặc sang một cụm mới. Khi phân tích $K \rightarrow \infty$ [Tài liệu 1,Neal 2000] ta có
- Nếu là cụm cũ trước đó: $\color{red} p(z_i = k | \mathbf{z}_{-i}, \alpha) \color{black} = \frac{ n_{k, -i} }{\alpha + N - 1}$
- Nếu là cụm mới: $\color{red} p(z_i = k^{*} | \mathbf{z}_{-i}, \alpha) \color{black} = \frac{ \alpha }{\alpha + N - 1}$
Và:
- $ \color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k, \lambda) \color{black} \propto \int p(x_i | \theta_k) \left[ \prod_{j \neq i, z_j = k} p(x_j | \theta_k) \right] H(\theta_k | \lambda) d \theta_k$
- $ \color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k^{*}, \lambda) \color{black} \propto \int p(x_i | \theta^{*}) \left[ \prod_{j \neq i, z_j = k} p(x_j | \theta^{*}) \right] H(\theta_k | \lambda) d \theta^{*} \\ = \int p(x_i | \theta^{*}) H(\theta^{*} | \lambda) d \theta^{*} = p(x_i | \lambda)$
Trong mô hình này, mỗi vòng lặp ngoài những cụm đang hiện hành ra thì chúng ta sẽ xét thêm liệu có nên thêm cụm mới vào. Dẫu $K \rightarrow \infty $ là một điều gì đó nghe như “phim kinh dị”, bởi vì chúng ta biết rằng hầu hết trong số chúng là những cụm không cần thiết, tuy nhiên may mắn thay hầu hết những cụm thừa không cần thiết sẽ bị loại bỏ sau một vài vòng lặp! Nếu những giả định của chúng ta là hợp lý với quá trình sinh dữ liệu, khi lặp đủ nhiều, mô hình này $K$ sẽ lặp quanh quẩn trong một khoảng nào đó.
Mã giả thuật toán:
$\mathtt{clusters} \leftarrow$ tạo $K$ cụm, mỗi cụm là một phân bố (cùng tiên nghiệm liên hợp tương ứng)
For $\mathtt{i}$ trong $1$ đến $N$ lặp: {
$z_i \leftarrow $lấy ngẫu nhiên thuộc từ $1$ đến $K$
Thêm $x_i$ vào cụm $\mathtt{clusters}[ z_i ]$, cập nhật các tham số cần thiết
}
For $\mathtt{iter}$ trong $1$ đến $\mathtt{maxiter}$ lặp: {
For $\mathtt{i}$ trong $1$ đến $N$ lặp: {
Xóa $x_i$ trong cụm $\mathtt{clusters}[ z_i ]$, cập nhật các tham số cần thiết
If cụm vừa xóa rỗng:
Xóa luôn cụm đó khỏi $\mathtt{clusters}$, cập nhật các tham số cần thiết
Tính và chuẩn hóa $\color{purple} p(z_i | \mathbf{z}_{-i}, \mathbf{x}, \alpha, \lambda)$, gọi phân bố rời rạc này là $p(z_{\mathtt{new}} | .)$
Lấy mẫu $z_{\mathtt{new}} \sim p(z_{\mathtt{new}} | .)$
If $z_{\mathtt{new}}$ là cụm mới:
Thêm một cụm mới vào $\mathtt{clusters}$, cập nhật các tham số cần thiết
Thêm $x_i$ vào cụm $\mathtt{clusters}[ z_{\mathtt{new}} ]$, cập nhật các tham số cần thiết
}
}
RETURN $z$
5. Thử cài đặt thuật toán DPMM với phân bố trộn Gaussian
Trong phần này chúng ta sẽ cài đặt DPMM (Dirichlet Process Mixture Model) cho phân bố Gaussian.
5.1 Tạo tập dữ liệu nhân tạo
import numpy as np
import scipy
from scipy import stats
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
# Hiện tại mình đang thiết một matplotlib style riêng
# khi nào hoàn tất mình sẽ chia sẻ :'>
plt.style.use('bmh')
# plt.style.use('thetalog')
np.random.seed(11)
s0 = 3.00 # độ lệch chuẩn giữa tâm các cụm
ss = 0.65 # độ lệch chuẩn giữa các điểm trong cụm
mean_1 = multivariate_normal.rvs(mean=np.array([0,0])) * s0
mean_2 = multivariate_normal.rvs(mean=np.array([0,0])) * s0
mean_3 = multivariate_normal.rvs(mean=np.array([0,0])) * s0
mean_4 = multivariate_normal.rvs(mean=np.array([0,0])) * s0
X1 = mean_1 + multivariate_normal.rvs(mean=np.array([0,0]), size=100) * ss
X2 = mean_2 + multivariate_normal.rvs(mean=np.array([0,0]), size=60) * ss
X3 = mean_3 + multivariate_normal.rvs(mean=np.array([0,0]), size=40) * ss
X4 = mean_4 + multivariate_normal.rvs(mean=np.array([0,0]), size=65) * ss
# nhãn cho các điểm dữ liệu thuộc về cụm tương ứng
truth = [0]*100 + [1]*60 + [2]*40 + [3]*65
X = np.concatenate((X1, X2, X3, X4))Vẽ X:
plt.scatter(X[:,0],X[:,1])
plt.show()
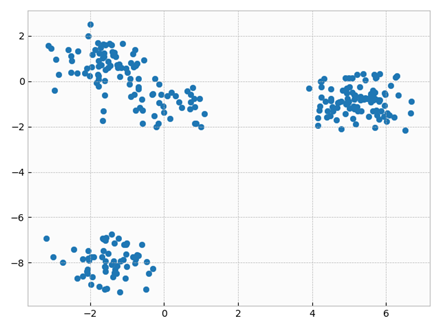
Vẽ X với nhãn của cụm:
plt.scatter(X1[:,0], X1[:,1])
plt.scatter(X2[:,0], X2[:,1])
plt.scatter(X3[:,0], X3[:,1])
plt.scatter(X4[:,0], X4[:,1])
plt.show()
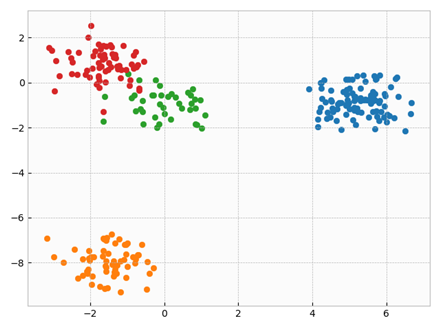
5.2 Cài đặt Gaussian (với Gaussian-Wishart làm phân bố tiên nghiệm)
Phần cài đặt phân bố $\color{blue} p(x_i | \mathbf{z}_{-i}, \mathbf{x}_{-i}, z_i = k, \lambda)$ với dùng phân bố cụm Gaussian (dùng Gaussian-Wishart làm tiên nghiệm cho tham số) cho từng phân bố con trong mô hình trộn.
Bạn đọc tham khảo phần chi tiết cài đặt: Tại đây
class _DPMulNormal:
"""
Lớp _DPMulNormal
Cài đặt phân bố Normal (Gaussian) nhiều chiều cho mô hình DPMM
(cùng tiên nghiệm liên hợp Gaussian-Wishart conjugate prior)
"""
def __init__(self, D=2, s0 = 5.0, ss = 0.65):
"""
Phương thức khởi tạo
:param D: int - số chiều
:param s0: float - độ lệch chuẩn giữa các cụm
:param ss: float - độ lệch chuẩn giữa các điểm trong cụm
"""
self.dd = D
self.vv = 5
self.vc = np.eye(D)
self.uu = np.zeros(shape=(D, 1))
self.nn = 0
self.ws = self.vc * self.vv
self.rr = 1.0 / (s0**2/ss**2)
self.cc = scipy.linalg.cholesky(self.ws + self.rr * self.uu @ self.uu.T)
self.xx = np.zeros(shape=(D,1))
def add_point(self, x):
"""
Thêm điểm
:param x: np.array - vectơ cột D x 1
"""
self.nn += 1
self.rr += 1
self.vv += 1
self.cc = self.__cholupdate(self.cc, x, '+')
self.xx += x
def del_point(self, x):
"""
Giảm điểm
:param x: np.array - vectơ cột D x 1
"""
self.nn -= 1
self.rr -= 1
self.vv -= 1
self.cc = self.__cholupdate(self.cc, x, '-')
self.xx -= x
def logpredictive(self, x):
"""
Log xác suất
:param x: np.array - vectơ cột D x 1
"""
dd = self.dd
nn = self.nn
rr = self.rr
vv = self.vv
cc = self.cc
xx = self.xx
lp = self.__z(dd,nn+1,rr+1,vv+1,self.__cholupdate(cc,x),xx+x) \
- self.__z(dd,nn, rr, vv ,cc ,xx)
return lp
def __cholupdate(self, R_current, x_update, sign='+'):
"""
Hàm bổ trợ phân rã Cholesky
+ Rank-one update
- Rank-one downdate
Giả sử R1 là kết quả của
R1 = cholesky_decomposition(A)
Ta muốn tìm kết quả
R2 = cholesky_decomposition(A + x @ x.T)
Thì thay vì tính toán lại từ đầu
R2 = __cholupdate(R1, x, '+')
(tương tự với trường hợp downdate)
:param R_current: np.array - lời giải trước
:param x_update: np.array - vectơ cập nhật (+x@x.T hoặc - x@x.T)
:param sign: str - '+' hoặc '-'
:return R: lời giải rank-one update (downdate) tương ứng
"""
R = R_current.copy()
x = x_update.copy()
n = len(x)
for k in range(n):
if sign == '+':
r = np.sqrt(R[k, k]**2 + x[k, 0]**2)
else:
r = np.sqrt(R[k, k]**2 - x[k, 0]**2)
c = r / R[k, k]
s = x[k, 0] / R[k, k]
R[k,k] = r
if k !=n-1:
if sign == '+':
R[(k+1):n, k] = (R[(k+1):n, k] + s * x[(k+1):n, 0]) / c
else:
R[(k+1):n, k] = (R[(k+1):n, k] - s * x[(k+1):n, 0]) / c
x[(k+1):n, 0] = c * x[(k+1):n, 0] - s * R[(k+1):n, k]
return R
def __z(self, dd, nn, rr, vv, cc, xx):
"""
Hàm bổ trợ để công thức nhìn gọn
"""
zz = - nn*dd/2*np.log(np.pi) - dd/2*np.log(rr) - \
vv*np.sum(np.log(np.diag(self.__cholupdate(cc, xx / np.sqrt(rr),'-')))) \
+ np.sum(scipy.special.loggamma((vv-(np.arange(0,dd, 1)))/2))
return zz5.3 Cài đặt trường hợp DP-GMM hữu hạn
Trong trường hợp DPMM hữu hạn, chúng ta sẽ khai báo số lượng $K$ cụm có trong mô hình.
def finite_dp_gmm(X, K, z_init=None, alpha=1.0, max_iters=100):
"""
(hữu hạn) Dirichlet Process - Gaussian Mixture Model
:param X: np.array - dữ liệu N x D (N dòng, D cột - chiều)
:param K: int - số cụm
:param z_init: np.array - nhãn của điểm khởi tạo
:param alpha: float - hệ số alpha độ tập trung
:param max_iters: int - số vòng lặp
:return z: kết quả phân cụm
"""
N = len(X)
D = X.shape[1]
n_points_cluster = np.zeros(K, dtype=int)
if z_init is None:
z = np.random.randint(0, K, size=N)
else:
z = z_init
# Mỗi cụm là một phân bố Gaussian nhiều chiều
clusters = [_DPMulNormal() for _ in range(K)]
# Khởi tạo thêm điểm vào cụm
for i in range(N):
c = z[i]
n_points_cluster[c] += 1
clus = clusters[c]
clus.add_point(X[i].reshape(D,1))
# Lặp
for _ in range(max_iters):
# Duyệt qua từng điểm dữ liệu
for i in range(N):
z_i = z[i]
x_i = X[i].reshape(D,1)
current_clus = clusters[z_i]
# Xóa điểm x_i ra khỏi cụm hiện tại
current_clus.del_point(x_i)
n_points_cluster[z_i] -= 1
# Tính xác suất theo hàm log rồi mũ lên
prob = np.log(alpha/float(K) + n_points_cluster)
for j in range(len(clusters)):
prob[j] = prob[j] + clusters[j].logpredictive(x_i)
prob = np.exp(prob - np.max(prob)) # ổn định tính toán số
prob = prob / prob.sum()
# Gieo ngẫu nhiên x_i thuộc về cụm nào, theo phân bố rời rạc prob
current_dist = stats.rv_discrete(values=(list(range(len(prob))), prob))
z_new = current_dist.rvs(size=1)
z_new = int(z_new)
# Thêm x_i vào cụm z_new
clusters[z_new].add_point(x_i)
n_points_cluster[z_new] += 1
z[i] = z_new
return zThử chạy thử xem:
np.random.seed(7)
K = 4
z = finite_dp_gmm(X, K, max_iters=50)Vẽ thử ra kết quả:
for c in np.unique(z):
plt.scatter(X[z==c,0], X[z==c,1])
plt.show()
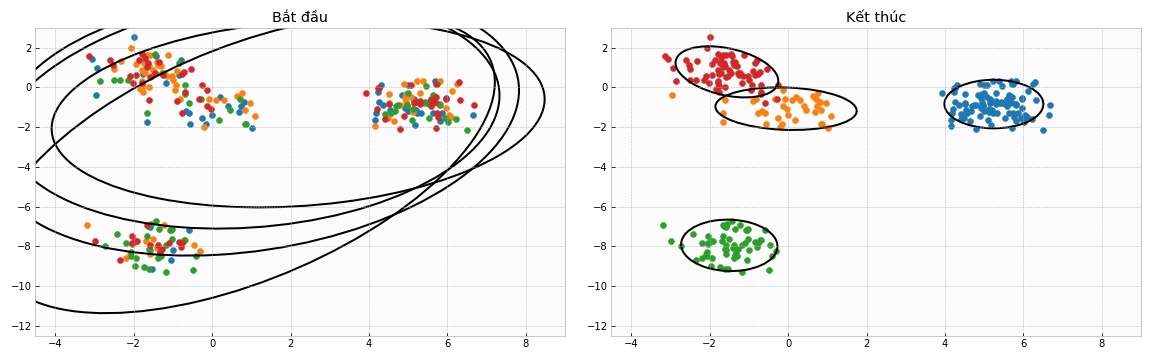
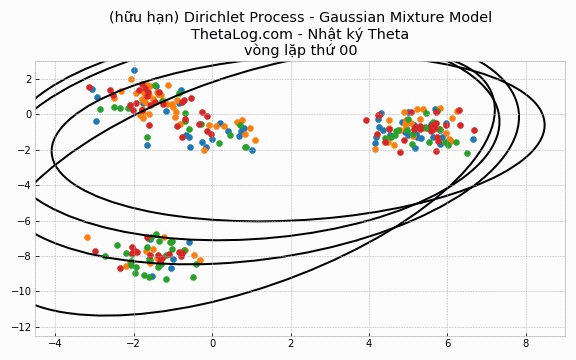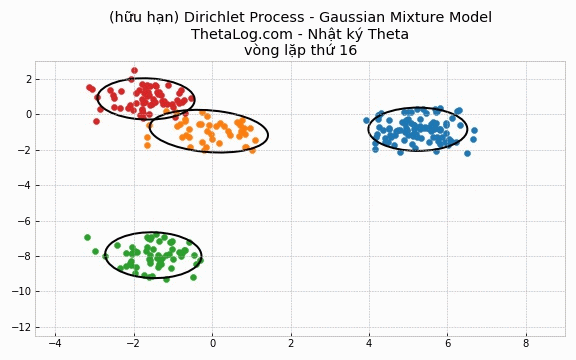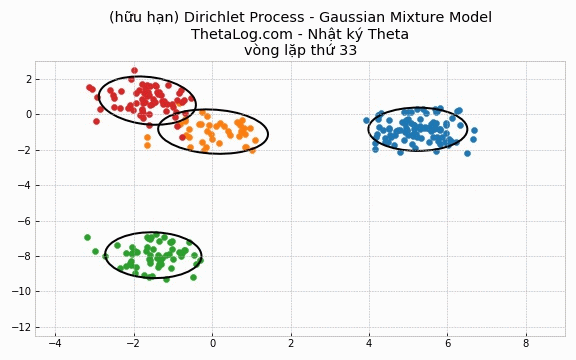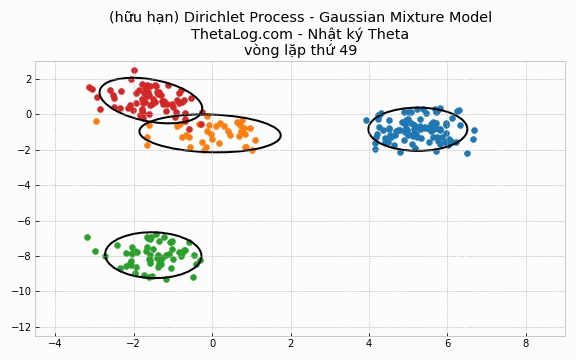
5.4 Cài đặt trường hợp DP-GMM vô hạn
Trong trường hợp DPMM vô hạn, chúng ta sẽ khai báo số lượng cụm $K$ là một số lớn ngay từ đầu.
def infinite_dp_gmm(X, K=25, z_init=None, alpha=1.0, max_iters=100):
"""
(vô hạn) Dirichlet Process - Gaussian Mixture Model
:param X: np.array - dữ liệu N x D (N dòng, D cột - chiều)
:param K: int - số cụm (khởi tạo là một con số rất lớn)
:param z_init: np.array - nhãn của điểm khởi tạo
:param alpha: float - hệ số alpha độ tập trung
:param max_iters: int - số vòng lặp
:return z: kết quả phân cụm
"""
N = len(X)
D = X.shape[1]
if z_init is None:
z = np.random.randint(0, K, size=N)
else:
z = z_init
K = len(np.unique(z))
n_points_cluster = [0] * K
# Mỗi cụm là một phân bố Gaussian nhiều chiều
clusters = [_DPMulNormal() for _ in range(K)]
dummy_dist = _DPMulNormal()
for i in range(N):
c = z[i]
n_points_cluster[c] += 1
clus = clusters[c]
clus.add_point(X[i].reshape(D, 1))
for _ in range(max_iters):
for i in range(N):
z_i = z[i]
x_i = X[i].reshape(D, 1)
current_clus = clusters[z_i]
# Xóa điểm x_i ra khỏi cụm hiện tại
current_clus.del_point(x_i)
n_points_cluster[z_i] -= 1
# Nếu cụm hiện tại không có bất kì điểm nào thì xóa hẳn nó
if n_points_cluster[z_i] == 0:
del n_points_cluster[z_i]
del clusters[z_i]
z[z > z_i] -= 1
# Tính xác suất theo hàm log rồi mũ lên
# Lưu ý: prob[-1], len(prob) = len(clusters) + 1
# prob[-1] là xác suất thêm cụm mới
prob = np.log(np.array(n_points_cluster + [alpha]))
for j in range(len(clusters)):
prob[j] = prob[j] + clusters[j].logpredictive(x_i)
prob[-1] = prob[-1] + dummy_dist.logpredictive(x_i)
prob = np.exp(prob - np.max(prob)) # ổn định tính toán số
prob = prob / prob.sum()
# Gieo ngẫu nhiên x_i thuộc về cụm nào, theo phân bố rời rạc prob
current_dist = stats.rv_discrete(values=(list(range(len(prob))), prob))
z_new = current_dist.rvs(size=1)
z_new = int(z_new)
if z_new == len(prob) - 1:
# Thêm cụm mới nếu z rơi vào cụm mới
clusters.append(_DPMulNormal())
n_points_cluster.append(0)
# Thêm điểm vào cụm
clusters[z_new].add_point(x_i)
n_points_cluster[z_new] += 1
z[i] = z_new
return zThử chạy thử xem:
np.random.seed(7)
# Mặc định K = 25
z = infinite_dp_gmm(X, max_iters=50)Vẽ thử ra kết quả:
for c in np.unique(z):
plt.scatter(X[z==c,0], X[z==c,1])
plt.show()
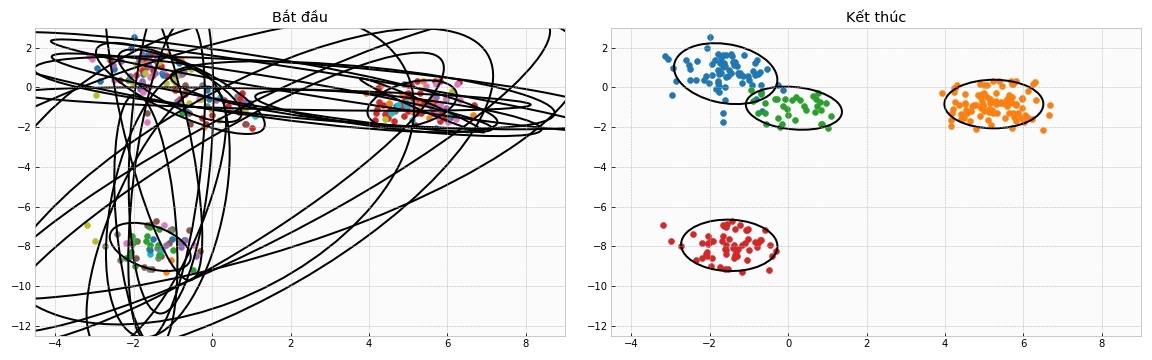
6. Phần kết
Github (chứa Jupyter Notebook): Tại đây
Trong bài viết này ThetaLog tìm hiểu và cài đặt DPMM với trường hợp Gaussian hay nói cách khác DP-GMM (Dirichlet Process Gaussian Mixture Model) qua MCMC (Collapsed Gibbs Sampling) có dùng tiên nghiệm liên hợp (conjugate prior) tương ứng. Những trường hợp khác không sử dụng tiên nghiệm liên hợp (conjugate prior) bạn đọc quan tâm có thể tìm hiểu qua [Tài liệu 1, Neal 2000]. Ngoài ra còn nhiều hướng giải quyết tìm tham số khác như biến phân (Variational Inference), sử dụng A* và Beam Search để tìm tham số,… bạn đọc quan tâm có thể tìm hiểu thêm.
Dirichlet Process Mixture Model là một mô hình phân cụm phi tham số thú vị. Hi vọng bài viết mang lại nhiều thông tin bổ ích cho bạn đọc! Chúc bạn có những giây phút vui vẻ bên thuật toán!
ThetaLog - Nhật ký Theta! Lê Quang Tiến - quangtiencs
Tham khảo
- Radford M. Neal. Markov Chain Sampling Methods for Dirichlet Process Mixture Models. Journal of Computational and Graphical Statistics. http://www2.stat.duke.edu/~scs/Courses/Stat376/Papers/DirichletProc/NealDirichletJCGS2000.pdf
- Kevin P. Murphy. Machine Learning A Probabilistic Perspective. The MIT Press. ISBN 978-0-262-01802-9
- Matt Gormley. The Dirichlet Process (DP) and DP Mixture Models. 10-708 Probabilistic Graphical Models. http://www.cs.cmu.edu/~epxing/Class/10708-16/slide/lecture18-DP.pdf
- Khalid El-Arini. Dirichlet Processes A gentle tutorial. https://www.cs.cmu.edu/~kbe/dp_tutorial.pdf
- Michael I. Jordan. Dirichlet Processes, Chinese Restaurant Processes, and all that. http://videolectures.net/icml05_jordan_dpcrp/
- Yee Whye Teh. Dirichlet Processes: Tutorial and Practical Course. https://www.stats.ox.ac.uk/~teh/teaching/npbayes/mlss2007.pdf
- Yee Whye Teh. Bayesian Nonparametrics. http://mlss.tuebingen.mpg.de/2013/2013/slides_teh.pdf
- Kurt Miller. Dr. Nonparametric Bayes Or: How I Learned to Stop Worrying and Love the Dirichlet Process. https://people.eecs.berkeley.edu/~jordan/courses/294-fall09/lectures/nonparametric/slides.pdf
- Eric Xing. Probabilistic Graphical Models. Bayesian Nonparametrics: Dirichlet Processes. http://www.cs.cmu.edu/~epxing/Class/10708-14/lectures/lecture19-npbayes.pdf