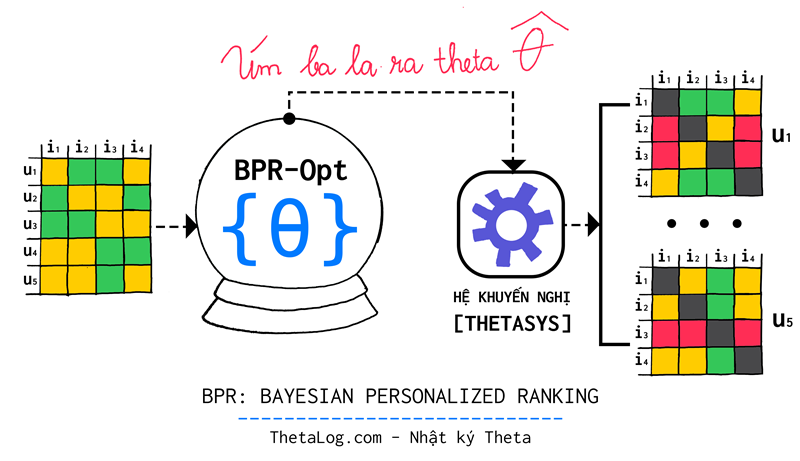
BPR Bayesian Personalized Ranking • Lê Quang Tiến

Bayesian Personalized Ranking (BPR) là một hướng tiếp cận để tối ưu tham số của một số mô hình hệ khuyến nghị thông dụng từ thông tin phản hồi tiềm ẩn được đề xuất bởi Rendle và cộng sự nhằm giải những khó khăn gặp phải bởi dữ liệu của bài toán này.

Hệ thống khuyến nghị (Recommender Systems, hoặc cũng có thể gọi Hệ gợi ý) là một chủ đề được nghiên cứu rất năng động. Trong bài toán này, thông tin mà chúng ta thu thập được có thể trong hai viễn cảnh sau đây:

Thông tin phản hồi rõ ràng (explicit feedback): người dùng đánh giá sản phẩm qua việc chấm điểm (ví dụ số sao ứng dụng).
Ưu điểm: thông tin được đưa ra trực tiếp từ người dùng (không phải tự phỏng đoán).
Nhược điểm: trải nghiệm người dùng rườm rà phức tạp, tiêu cực từ thành kiến người dùng (ví dụ: một sản phẩm bị đánh giá ¹⁄₅ sao ngay từ đầu khả năng cao là sẽ ít được người khác ngó ngàng tới nữa).
Thông tin phản hổi tiềm ẩn (implicit feedback): người dùng xem sản phẩm, tương tác với sản phẩm,…
Ưu điểm: mọi thông tin có thể thu thập ngầm mà không gây phiền đến người dùng.
Nhược điểm: suy luận theo kiểu phỏng đoán, thông tin không rành mạch.

Trong công nghiệp, hệ khuyến nghị đóng vai trò quan trọng trong tăng doanh thu dịch vụ (ví dụ: dự đoán mặt hàng người dùng muốn mua trong thương mại điện tử, nhạc & phim với các dịch vụ giải trí,…). Hầu hết các ứng dụng thông thường chọn hướng tiếp cận thu thập thông tin phản hồi tìm ẩn, ví như “mua” từ Amazon, “click” từ “Google Advertisement”, “thả tim” từ “Instagram”…

Trong bài viết này, chúng ta sẽ tìm hiểu những khó khăn của bài toán xây dựng hệ khuyến nghị từ thông tin phản hồi tiềm ẩn từ người dùng, đồng thời tìm hiểu hướng tiếp cận Bayesian Personalized Ranking (BPR) giải quyết bài toán này ra sao!

1. Vì sao huấn luyện một hệ khuyến nghị lại khó?

Giả sử bạn sở hữu một trang web thương mại điện tử lớn ThetaShop. Mỗi lần người dùng vào xem một sản phẩm sẽ có hàng loạt gợi ý những sản phẩm khác, hy vọng rằng những sản phẩm mà chúng ta gợi ý sẽ là những sản phẩm mà người dùng muốn mua. Như vậy, nếu hệ khuyến nghị hoạt động hiệu quả thì doanh thu của ThetaShop sẽ tăng đáng kể!

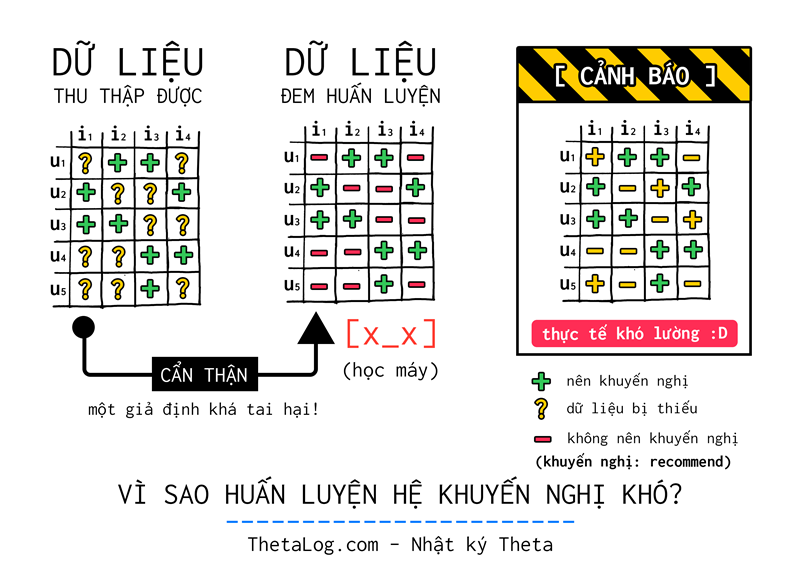
Những kỹ sư khoa học dữ liệu sẽ là những người đi xây dựng các mô hình toán học cho các hệ khuyến nghị này. Thật không may, một tình huống đáng tiếc xảy ra, bài toán của chúng ta bị ảnh hưởng bởi dữ liệu thu thập rất nhiều!

Trong bài toán này, thông thường bạn chỉ thu thập được dữ liệu trường hợp nào “nên khuyến nghị” (mang tính tích cực), hầu như không, ít khi bạn thu thập hoặc nhận biết được dữ liệu trường hợp nào “không nên khuyến nghị” (mang tính tiêu cực). (vì thế đôi lúc người ta gọi đây là bài toán một lớp one class recommender system vì chỉ có một loại thông tin có thể quan sát được)

Giả sử bài toán như sau:

ThetaShop có $4$ sản phẩm khác nhau, gọi đó là tập $I = \{ i_1, i_2, i_3, i_4 \}$ với $I$ là tập sản phẩm (items).
ThetaShop có $5$ người dùng, gọi đó là tập $U = \{ u_1, u_2, u_3, u_4, u_5 \}$ với $U$ là tập người dùng (users).

Và lúc này kí hiệu:

$ \color{green} \mathbf{+}$: những trường hợp nên khuyến nghị (ví dụ tương tác người dùng $u_1$ mua sản phẩm $i_2$).
$\color{yellow} \mathbf{?}$: những trường bị thiếu do không quan sát được. Liệu chúng ta có thể kết luận gì?
$\color{red} \mathbf{-}$: những trường hợp không nên khuyến nghị (vì có lẽ người dùng sẽ không thích sản phẩm này).

Thực tế khó lường, rất chi phũ phàng
$\color{yellow} \mathbf{?}$: số lượng trường hợp không quan sát được là rất nhiều. Hơn nữa những gì không biết rất khó kết luận, chúng ta không thể đoán bừa được! Người dùng không tương tác, biết đâu là vì chưa bao giờ từng biết về sản phẩm này, nhưng nếu gặp khả năng thích là rất cao?!? $\color{red} \mathbf{-}$: hầu như không hoặc khó thu thập được những trường hợp này (khi mọi thứ thu thập ngầm).

Thực tế khó lường, rất chi phũ phàng

$\color{yellow} \mathbf{?}$: số lượng trường hợp không quan sát được là rất nhiều. Hơn nữa những gì không biết rất khó kết luận, chúng ta không thể đoán bừa được! Người dùng không tương tác, biết đâu là vì chưa bao giờ từng biết về sản phẩm này, nhưng nếu gặp khả năng thích là rất cao?!?
$\color{red} \mathbf{-}$: hầu như không hoặc khó thu thập được những trường hợp này (khi mọi thứ thu thập ngầm).

Thông thường, các thuật toán máy học cho mô hình khuyến nghị cổ điễn thường giả định những trường hợp không quan sát được là những trường hợp không nên khuyến nghị. Tất nhiên, nếu học trên dữ liệu như thế sẽ làm hệ khuyến nghị trở nên “quá khớp” (overfitting), hay nói cách khác dự đoán trên tập dữ liệu huấn luyện rất tốt nhưng trên dữ liệu chưa bao giờ nhìn thấy rất tệ. Phần lớn các thuật toán đều có một số giải pháp để tránh việc này thông qua “bình thường hóa” (regularization).

Tuy nhiên chúng ta ở đây sẽ tìm hiểu một hướng tiếp cận khá thú vị với bài toán này Bayesian Personalized Ranking!

2. Bayesian Personalized Ranking

Một cửa hàng ThetaShop trực tuyến muốn đưa ra danh sách các sản phẩm mà người dùng muốn mua.

Gọi:

$U$: tập tất cả người dùng. Ví dụ: $U = \{ u_1, u_2, u_3, u_4, u_5 \}$
$I$: tập tất cả sản phẩm. Ví dụ: $I = \{ i_1, i_2, i_3, i_4 \}$

Trong viễn cảnh này $S \subseteq U \times I$ là tập phản hồi từ người dùng.

Tác vụ của hệ khuyến nghị (recommender system) là đưa ra xếp hạng được cá nhân hóa cho người dùng $u$ những sản phẩm mà người dùng $u$ có thể yêu thích.

Một xếp hạng các sản phẩm, có thể định nghĩa bằng một quan hệ toán học, quan hệ toán học ở đây trả lời cho câu hỏi có hay không quan hệ giữa hai đối tượng đang xét, gọi quan hệ trên là $>_u \subset I^2$ của tất cả sản phẩm. Lúc này ta ký hiệu $ i >_u j$ khi người dùng $u$ thích sản phẩm $i$ hơn sản phẩm $j$.
(lưu ý: ở đây $>_u$ xem như một ký hiệu, tránh nhầm lẫn, bài viết này dựa trên hệ ký hiệu bài viết gốc)

Quan hệ này thỏa:

$\forall i,j \in I : i \neq j \Rightarrow i >_u j \lor j >_u i$
[ totality - toàn phần ] Sản phẩm $i$ và $j$ nằm một trong hai trường hợp $i$ được thích hơn $j$, hoặc sản phẩm $j$ được thích hơn $i$.
$\forall i,j \in I: i >_u j \land j >_u i \Rightarrow i = j$
[ antisymmetry - phi đối xứng ] Quan hệ phi đối xứng, nếu thích $i$ hơn $j$ thì không thể xảy ra $j$ thích hơn $i$. Do đó ta quy định rằng nếu điều trên xảy ra thì $i$ và $j$ là một sản phẩm $i=j$.
$\forall i,j,k \in I: i >_u j \land j >_u k \Rightarrow i >_u k$
[ transitivity - tính bắc cầu ] Quan hệ bắt cầu, nếu người dùng thích sản phẩm $i$ hơn $j$ và thích sản phẩm $j$ hơn $k$ thì ta có thể suy ra người dùng thích $i$ hơn $k$.

Để tiện lợi hơn, chúng ta cũng định nghĩa:

$$I_u^{+} := \{ i \in I : (u,i) \in S \}$$ $$ U_i^{+} := \{ u \in I : (u,i) \in S \}$$

(ở đây $I_u^{+}$ là tập những sản phẩm mà người dùng $u$ đã thích (mua, thả tim,..), tương tự $U_i^{+}$ là tập người dùng có tương tác với sản phẩm $i$ hệ thống)

Thay vì tiếp cận theo hướng cũ, giả định toàn bộ trường hợp không quan sát được là trường hợp “không nên khuyến nghị”, hướng tiếp cận của BPR đặt ra một bài toán tối ưu hoàn toàn mới!

Gọi $D_S$ là dữ liệu huấn luyện ban đầu:

$$D_S = \{ (u,i,j) | i \in I_u^+ \land j \in I \setminus{I_u^+} \}$$

Tập $D_S$ là một tập gồm các bộ $(u,i,j)$, ngữ nghĩa của các bộ $(u,i,j)$ ở đây là người dùng $u$ thì được giả định là thích $i$ hơn $j$ vì người dùng đã tương tác với $i$ mà không thấy tương tác gì với $j$.

Hướng tiếp cận này có hai ưu điểm chính:

Dữ liệu huấn luyện bao gồm các cặp (nên khuyến nghị - không nên khuyến nghị) và những trường hợp các cặp dữ liệu bị thiếu không đầy đủ sẽ không được đưa vào quá trình huấn luyện.
Dữ liệu huấn luyện được tạo bởi mục tiêu xếp hạng (mục tiêu tối ưu này phù hợp với bài toán hơn) so với việc giả định ở các hướng tiếp cận cổ điển.

2.1 Bài toán tối ưu BPR Optimization Criterion

Giả sử chúng ta có một tập tham số $\Theta$, tập tham số biểu diễn vector tham số của một mô hình khuyến nghị (ví dụ Matrix Factorization).

Theo công thức Bayes, phân bố xác suất hậu nghiệm:

$$p(\Theta | >_u ) = \frac{p(>_u | \Theta) p(\Theta)}{p(>_u)}$$

Do $p(>_u)$ đóng vai trò như hằng số chuẩn hóa, do đó ta có thể viết phân bố hậu nghiệm lại ở dạng tỷ lệ:

$$p(\Theta | >_u ) \propto \color{WildStrawberry} p(>_u | \Theta) \color{RoyalBlue} p(\Theta)$$

Ký hiệu $>_u$ được xem như là cấu trúc về sự ưa thích của người dùng $u$.

Phần sau đây, có lẽ sẽ có nhiều mẹo mực là chủ yếu, lý thuyết đẹp đẽ ngay từ đầu dường như không phải là trường hợp của bài này. Tuy nhiên, không cần cao siêu phức tạp, miễn giải quyết được tốt vấn đề thì nó vẫn là lời giải đẹp!

GIẢ ĐỊNH 1: Tất cả người dùng hành động độc lập lẫn nhau.

Vì tất cả người dùng được giả định hành động độc lập lẫn nhau. Chúng ta có thể viết hàm triển vọng (likelihood function trong công thức Bayes) lại dưới dạng tích:

$$ \prod_{w \in U} p(>_w | \Theta)= p(>_{u_1} | \Theta) p(>_{u_2} | \Theta)…p(>_{u_n} | \Theta) $$

GIẢ ĐỊNH 2: Sự sắp xếp của các cặp $(i, j)$ trong quan hệ người dùng $w$ thích $i$ hơn $j$ là độc lập lẫn nhau.

Do đó ta có thể viết lại với mỗi người dùng $w \in U$:

$$ p( >_w | \Theta) = \prod_{(w,i,j) \in U \times I \times I } p(i >_w j | \Theta)^{\delta ((w,i,j) \in D_S)} \dot (1 - p(i >_w j | \Theta))^{\delta ((w,i,j) \notin D_S)}$$

Với $\delta$ là hàm thuộc tính (indicator function):

$$ \delta(s) = \left\{ { \begin{array}{*{20}{c}}{1}&{\text{nếu mệnh đề } s \text{ đúng}}\\ 0 &{\text{còn lại}}\end{array} } \right. $$

Đại ý ở đây mỗi tích $p(i >_w j | \Theta)^{\delta ((w,i,j) \in D_S)} \dot (1 - p(i >_w j | \Theta))^{\delta ((w,i,j) \notin D_S)}$ là khả năng mà người dùng $w$ thích sản phẩm $i$ hơn sản phẩm $j$.

Vì tính [ totality - toàn phần ] và [ antisymmetry - phi đối xứng ] ta có thể đơn giản công thức về:

$$p(>_w | \Theta) = \prod_{(w,i,j) \in D_S} p(i >_w j | \Theta)$$

Lúc này để ý, vì chúng ta đang xét những trường hợp những bộ $(w, i, j) \in D_S$, nên lúc này một quan hệ $ i >_w j$ bất kì:

$$ p(i >_w j | \Theta) = \left\{ { \begin{array}{*{20}{c}}{1}&{\text{nếu } i >_w j }\\ 0 &{\text{còn lại}}\end{array} } \right. $$

Vì thế chúng ta cần tìm cách “làm mềm” bài toán tại đây. Nếu không thì $p(>_w | \Theta)$ chỉ là $0$ hoặc $1$ mà thôi!

Đặt

$$ p(i >_w j | \Theta) = \sigma (\hat{x}_{wij}(\Theta))$$

Với $\sigma$ là hàm sigmoid:

$$ \sigma (x) = \frac{1}{1+e^{-x}} $$

Với $\hat{x}_{wij} (\Theta)$ là một giá trị thực của hàm số theo tham số $\Theta$ từ mô hình hệ khuyến nghị mà ta đang dùng thể hiện mức độ mà người dùng $u$ thích sản phẩm $i$ hơn $j$, ở đây chúng ta xây dựng một mô hình linh hoạt có thể dùng cho nhiều mô hình bên dưới khác nhau.

Để tiện lợi, dể theo dõi hơn từ phần này về sau $\hat{x}_{wij}$ hiểu ngầm là $\hat{x}_{wij} (\Theta)$.

Lúc này ta có thể hoàn tất viết hàm triển vọng dưới dạng:

$$ \color{WildStrawberry} p(>_u | \Theta ) = \prod_{(u,i,j) \in D_S } \sigma (\hat{x}_{uij})$$

Chúng ta đã bàn về hàm triển vọng, để hoàn tất mô hình suy luận Bayesian chúng ta cần thêm tiên nghiệm $\color{RoyalBlue} p(\Theta)$, xem $\Theta$ như một vectơ ngẫu nhiên có phân bố chuẩn nhiều chiều $\Theta \sim \mathcal{N}(0, \Sigma_{\Theta})$ với trung bình tại gốc tọa độ $\mu = 0$ và ma trận hiệp phương sai $\Sigma_{\Theta}$, lúc này phân bố của $\Theta$:

$$ \color{RoyalBlue} p(\Theta) = \mathcal{N}(\Theta | 0, \Sigma_{\Theta})$$

Vì ta mong muốn tìm một $\Theta$ khả năng xảy ra là cao nhất khi quan hệ $>_u$ xảy ra, tức tìm $\Theta$ sao cho:

$$ \underset{\Theta}{\operatorname{argmax}} p(\Theta | >_u ) $$

Tuy nhiên thay vì tối ưu trực tiếp, để tối ưu phân bố xác suất, chúng ta có thể dùng log loss để tối ưu nhanh hơn (vì sao? Đọc thêm về Cross Entropy trong Lý Thuyết Thông Tin - Information Theory). Đặt:

$$ \begin{align} \mathtt{BPR-Opt} & = \ln{p(\Theta | >_u)} \\ & = \ln{ \left[ \color{WildStrawberry} p(>_u | \Theta ) \color{RoyalBlue} p(\Theta) \right] } \\ & = \ln{ \left[ \color{WildStrawberry} \prod_{(u,i,j) \in D_S } \sigma (\hat{x}_{uij}) \color{RoyalBlue} p(\Theta) \right] } \\ & = \sum_{(u,i,j) \in D_S } \ln{\sigma (\hat{x}_{uij})} + \ln{p(\Theta)} \end{align} $$

Đến đây, vẫn còn một ít “mẹo” cần vượt qua, tạm thời tại đây chúng ta xem như $\Sigma_{\Theta} = \lambda \mathbf{I} $, và $\Theta$ là một vectơ ngẫu nhiên $d$ chiều, do đó lúc này ta có:

$$ \begin{align} p(\Theta ) & = \frac{1}{(2 \pi)^{d/2} \sqrt{|\Sigma_{\Theta} |}} \exp{\left( -\frac{1}{2} (\Theta - \mu)^{\intercal} \Sigma^{-1}_{\Theta} (\Theta - \mu) \right)} \\ &= \frac{1}{(2 \pi)^{d/2} \sqrt{\lambda^{d}}} \exp{\left( -\frac{1}{2 \lambda} \Theta^{\intercal} \Theta \right)}\end{align}$$

Vì ta biết $| k A | =k^d | A |$ (với $A$ là ma trận $d \times d$ và $|A|$ là định thức của $A$) do đó $|\Sigma_{\Theta}| = |\lambda \mathbf{I} | = \lambda^d | \mathbf{I} | = \lambda^d$ và $\Sigma_{\Theta}^{-1} = \frac{1}{\lambda} \mathbf{I}$.

Do đó:

$$ \begin{align} \ln{p(\Theta)} &= \ln{ \left[ \frac{1}{(2 \pi)^{d/2} \sqrt{\lambda^{d}}} \exp{\left( -\frac{1}{2 \lambda} \Theta^{\intercal} \Theta \right)} \right]} \\ &= \color{orange} \ln{ \left[ \frac{1}{(2 \pi)^{d/2} \sqrt{\lambda^{d}}} \right]} \color{#37474f} + \ln{\left[ \exp{\left( -\frac{1}{2 \lambda} \Theta^{\intercal} \Theta \right)} \right]} \\ &= -\frac{1}{2 \lambda} \Theta^{\intercal} \Theta + \color{orange} \ln{ \left[ \frac{1}{(2 \pi)^{d/2} \sqrt{\lambda^{d}}} \right]}\end{align} $$

Đặt $\lambda_{\Theta} = \frac{1}{2 \lambda} $ lúc này xem đây như là tham số bình thường hóa mô hình, lúc này biểu thức màu cam sẽ là một hằng số phụ thuộc $\lambda_{\Theta}$ mà ta thêm vào, ta có:

$$ \ln{p(\Theta)} = -\lambda_{\Theta} || \Theta ||^2 + \color{orange} \text{constant}$$

Do đó bài toán tối ưu chúng ta qui về tìm cực đại của:

$$ \mathtt{BPR-Opt} = \sum_{(u,i,j) \in D_S } \ln{\sigma (\hat{x}_{uij})} - \lambda_{\Theta} || \Theta ||^2 $$

2.2 Thuật toán học BPR

BPR có hàm tối ưu mục tiêu là hàm khả vi, do đó chúng ta có thể dựa trên thuật toán hạ dốc (gradient descent) để xây dựng một phiên bản thuật toán tối ưu để cực đại $\mathtt{BPR-Opt}$.

Tuy nhiên do số lượng phần tử của tập $D_S$ có đâu đó khoảng $|S|\times |I|$ bộ $(u,i,j)$ huấn luyện nên nếu dựa trên thuật toán hạ dốc gốc thông thường sẽ chạy rất chậm. Hơn nữa hãy tưởng tượng trường hợp sau, người dùng $u$ thích $i$ hơn phần lớn các trường hợp $j$ có trong tập dữ liệu (ví dụ chỉ mới mua mỗi $i$), nó dẫn đến vectơ gradient sẽ tương đối lớn, việc này dẫn đến chúng ta phải chọn một hệ số học learning rate đủ nhỏ (phụ thuộc nhiều vào dữ liệu), hơn nữa việc bình thường hóa chọn tham số regularization $\lambda_{\Theta}$ cũng sẽ khó hơn.

Do đó, hướng tiếp cận mà BPR sử dụng là SGD (stochastic gradient descent), thuật toán BPR tổng quát:

FUNCTION LearnBPR$(D_S, \Theta)$:
Khởi tạo $\Theta$
While chưa hội tụ:
$(u,i,j) \leftarrow$ chọn ngẫu nhiên từ $D_S$
$\Theta \leftarrow \Theta + \alpha \left( \frac{e^{-\hat{x}_{uij}}}{1+e^{-\hat{x}_{uij}}} \cdot \frac{\partial}{\partial \Theta} \hat{x}_{uij} + \lambda_{\Theta} \cdot \Theta \right)$
Endwhile
RETURN $\Theta$

Trong trường hợp mini-batch tại mỗi vòng lặp chúng ta tính vector gradient cho batch điểm.

2.3 Học mô hình hệ khuyến nghị với BPR

Bởi vì quá trình tối ưu của chúng ta dựa trên tập dữ liệu sinh ra từ các bộ $(u,i,j) \in D_S$, tuy nhiên hầu hết kết quả đầu ra của các thuật toán cổ điển không phải là một giá trị $\hat{x}_{uij}$ do đó chúng ta cần phải chuyển bài toán về dạng thích hợp hơn. Xem

$$\hat{x}_{uij} = \hat{x}_{ui} - \hat{x}_{uj} $$

Với $\hat{x}_{ui}$ là giá trị thể hiện mức độ yêu thích của người dùng $u$ với sản phẩm $i$.

2.3.1 (BPR-MF) BPR cho Matrix Factorization

Với các hệ Matrix Factorization, bài toán dự đoán $\hat{x}_{ui}$ có thể được xem như là tác vụ ước lượng một ma trận $\hat{X}$ kích thước $|U| \times | I |$ được phân tích thành hai ma trận $W$ (kích thước $|U| \times k$) và $H$ (kích thước $|I| \times k$) thỏa:

$$ \hat{X} \approx WH^{\intercal} $$

Matrix factorization giả định rằng:

Mỗi người dùng và sản phẩm có thể được mô tả bởi $k$ đặc trưng.
$k$ đặc trưng ở đây có thể hiểu như là những nhân tố ở bên dưới thể hiện mối liên hệ giữa người dùng và sản phẩm. Ví dụ: hệ khuyến nghị về phim, $k$ đặc trưng có thể là: “hài hước”, “viễn tưởng”, “chiến tranh”, “tâm lý”,…

Với bài toán này, công thức dự đoán về độ yêu thích sản phẩm $i$ của người dùng $u$ được tính bởi:

$$ \hat{x}_{ui} = \sum_{f=1}^k w_{uf} \cdot h_{if} $$

Tham số mô hình cho bài toán này là $\Theta = (W, H)$. (với các phương pháp cổ điển chúng ta có thể giải quyết bài toán này với FunkMF, SVD++,…)

Với hướng tiếp cận BPR-MF chúng ta sẽ tìm $\Theta$ qua việc tối ưu $\mathtt{BPR-Opt}$, với thuật toán LearnBPR$(D_S, \Theta)$ giờ đây chúng ta chỉ còn thiếu $\frac{\partial}{\partial \Theta} \hat{x}_{uij}$.

Đặt $\theta$ là một phần tử trong ma trận $\Theta = (W,H)$. Ta có:

$$ \frac{\partial}{\partial \theta} \hat{x}_{uij} = \left\{ { \begin{array}{*{20}{c}}{ (h_{if} - h_{jf})}&{\text{nếu } \theta \text{ là } w_{uf}} \\ w_{uf} & {\text{nếu } \theta \text{ là } h_{if}} \\ -w_{uf} & {\text{nếu } \theta \text{ là } h_{jf}} \\ 0 & { \text{ còn lại }}\end{array} } \right. $$

(mình không thích ký hiệu theo cách này của bài báo gốc cho lắm :D, lưu ý lúc này $\Theta$ là một ma trận kích thước $(|U| + |I|) \times k$, với $f$ trong công thức trên là cột của ma trận $\Theta$)

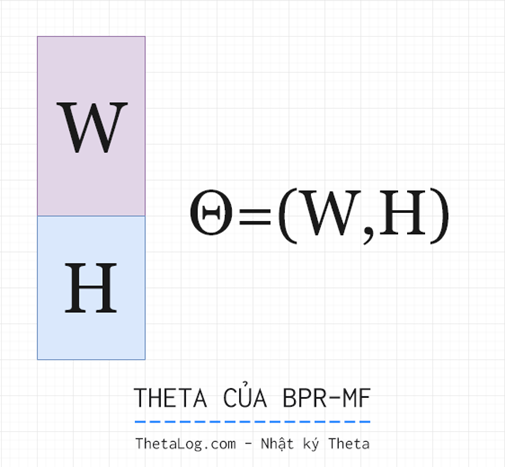
2.3.2 (BPR−kNN) BPR cho các hệ k người láng giềng

Bạn đọc quan tâm, có thể tìm đọc thêm bài báo gốc. ThetaLog sẽ không trình bày ở đây, vì có vẻ như hướng tiếp cận BPR cho hệ này không tăng hiệu quả của mô hình này. Nhưng cũng biết đâu bất ngờ, với vài tinh chỉnh, thuật toán này sẽ chạy tốt thì sao? :D

3. Thử cài đặt thuật toán BPR-MF và chạy thử trên tập dữ liệu MovieLens 100K

Dẫu thuật toán này xây dựng để giải quyết cho các bài toán hệ khuyến nghị tiềm ẩn. Tuy nhiên chúng ta vẫn có thể dùng để khuyến nghị cho các hệ phản hồi rõ ràng! Với những phản hồi rõ ràng, chúng ta chỉ cần chọn một ngưỡng để xem đó là những phản hồi tích cực nên khuyến nghị (ví dụ số sao >=3 chẳng hạn). Trong thực tế thì các hệ khuyến nghị đôi lúc kết hợp cả hai dạng thông tin để thu lại kết quả tốt nhất.

Nếu như bạn đang tìm một phiên bản cài đặt thuật toán BPR tốt bạn có thể tìm ở PreferredAI - cornac, có thể cài từ kênh conda-forge (với phân phối Anaconda Python).

Một phần mã nguồn tiền xử lí dữ liệu, đánh giá có tham khảo cài đặt từ Ethen (MingYu) Liu [5] với một vài chỉnh sửa mã nguồn tinh gọn, dể bảo trì hơn.

Phần learn_bpr_mf_mini_batch và learn_bpr_mf_sgd được cài đặt từ trang giấy trắng, trong thực hành thực tế, bạn chỉ cần chạy một thuật toán là đủ.

(thực ra thì learn_bpr_mf_sgd là phiên bản của learn_bpr_mf_mini_batch với batch=1 nhưng vì muốn giữ một phiên bản nguyên tác của bài báo nên mình thêm thuật toán learn_bpr_mf_sgd vào)

# Load các thư viện cần thiết
import os
import math
import numpy as np
import pandas as pd
from urllib.request import urlopen
from zipfile import ZipFile
from scipy.sparse import csr_matrix, dok_matrix
from sklearn.metrics import roc_auc_score

np.random.seed(12)

3.1 Tải dữ liệu từ mạng

def load_movielens_data():
    """
    Tải tập tin dữ liệu từ trang chủ grouplens
    Tập dữ liệu: ml-100k
    
    :return dataframe: pandas df
    """
    zipurl = 'http://files.grouplens.org/datasets/movielens/ml-100k.zip'
    zipresp = urlopen(zipurl)
    
    # Nếu không có thì tài về từ mạng internet
    if not os.path.isdir('ml-100k'):
        print('Downloading: http://files.grouplens.org/datasets/movielens/ml-100k.zip')
        with open("ml-100k.zip", "wb") as file:
            file.write(zipresp.read())
            file.close()
        print('Completed!')
    
    # Giải nén
    zipdata = ZipFile("ml-100k.zip")
    zipdata.extractall(path = '')
    zipdata.close()
    
    # Load dữ liệu từ Pandas
    file_path = os.path.join('ml-100k', 'u.data')
    names = ['users', 'items', 'ratings', 'timestamp']
    dataframe = pd.read_csv(file_path, sep = '\t', names = names)
    return dataframe

dataframe = load_movielens_data()

# Xem thử dữ liệu trông thế nào
dataframe.head()

	users	items	ratings	timestamp
0	196	242	3	881250949
1	186	302	3	891717742
2	22	377	1	878887116
3	244	51	2	880606923
4	166	346	1	886397596

3.2 Chuyển từ DataFrame ban đầu sang ma trận bài toán BPR

def convert_to_bpr_mat(dataframe, threshold=3):
    """
    Chuyển đổi DataFrame MovieLens 100K ban đầu sang ma trận BPR
    Mỗi dòng là Users
    Mỗi cột là Item
    Định dạng ma trận thưa
    
    :param dataframe: pandas df movielens 100K
    :param threshold: ngưỡng ratings chấp nhận nên khuyến nghị 
    :return bpr_mat: np.array - ma trận thưa bpr
    """
    tempdf = dataframe.copy()
    tempdf['positive'] = tempdf['ratings'].apply(func=lambda x: 0 if x < threshold else 1)
    
    # Vì tập dữ liệu này đánh index từ 1 nên chuyển sang kiểu category
    # để tránh việc chúng ta có ma trận 
    tempdf['users'] = tempdf['users'].astype('category')
    tempdf['items'] = tempdf['items'].astype('category')
    
    bpr_mat = csr_matrix((tempdf['positive'],
                          (tempdf['users'].cat.codes, 
                           tempdf['items'].cat.codes)))
    bpr_mat.eliminate_zeros()
    del tempdf
    return bpr_mat

bpr_mat = convert_to_bpr_mat(dataframe)

3.3 Tách ra thành tập dữ liệu Train & Test

def split_to_train_test(bpr_mat, test_ratio = 0.2, verbose=True):
    """
    Chia tập dữ liệu ra thành tập train & tập test
    
    :param bpr_mat: ma trận bpr
    :param test_ratio: float - tỉ lệ test set
    
    :return train: ma trận bpr train
    :return test: ma trận bpr test
    """
    # Số lượng người dùng
    n_users = bpr_mat.shape[0]
    # Dùng ma trận thưa Dictionary Of Keys tối ưu hơn cho công đoạn này
    train = bpr_mat.copy().todok()
    test = dok_matrix(train.shape) # Lưu ý hiện tại test là ma trận 0
    
    # với mỗi người dùng u
    # chia số trường hợp nên khuyến nghị với tỉ lệ test_ratio đươc cho
    # phần nào thuộc về test
    for u in range(n_users):
        split_index = bpr_mat[u].indices
        # đếm số trường hợp nên khuyến nghị
        count_positive = split_index.shape[0]
        n_splits = math.ceil(test_ratio * count_positive)
        test_index = np.random.choice(split_index, size=n_splits, replace=False)
        # Xem như dữ liệu chưa biết trong tập train
        train[u, test_index] = 0
        # Xem như dữ liệu nhìn thấy trong tập test
        test[u, test_index] = 1
    
    train, test = train.tocsr(), test.tocsr()
    
    # Nếu cần in thông tin ra ngoài
    if verbose:
        print('BPR matrix with %d stored elements' % bpr_mat.nnz)
        print('Train matrix with %d stored elements' % train.nnz)
        print('Test matrix with %d stored elements' % test.nnz)
    return train, test

bpr_train, bpr_test = split_to_train_test(bpr_mat, test_ratio=0.2, verbose=True)

Màn hình in ra thông tin:

BPR matrix with 82520 stored elements
Train matrix with 65641 stored elements
Test matrix with 16879 stored elements

3.4 Hàm bổ trợ (dự đoán, khuyến nghị, đánh giá)

def predict_bpr(W, H, user=None):
    """
    Hàm trả về X_hat
    
    :param W: ma trận W từ MF
    :param H: ma trận H từ MF
    :param user: người dùng (nếu None mặt định trả về tất cả)
    
    :return predict_scores: điểm dự đoán từ BPR MF
    """
    if user is None:
        return W @ H.T
    else:
        return W[user] @ H.T

def recommend_bpr(bpr_matrix, predict_score, user, n_rmd_items=None):
    """
    Dự đoán những sản phẩm mà người dùng muốn mua
    Những sản phẩm nào đã thích rồi thì không trả về nữa
    Trả về index theo bpr_matrix (đánh từ 0)
    
    :param bpr_matrix: ma trận bpr hiện tại
    :param predict_score: điểm dự đoán các item
    :param user: số thứ tự người dùng của predict score
    :param n_rmd_items: số lượng sản phẩm trả về, mặc định tất cả
    
    :return rmd_items: danh sách các sản phẩm khuyến nghị
    """
    # Số lượng sản phẩm
    n_items = bpr_matrix.shape[1]
    # những sản phẩm đã thích rồi
    liked_items = bpr_matrix[user].indices
    scores = predict_score.copy()
    
    # index ban đầu khi chưa sắp xếp
    sort_index = np.arange(0, n_items)
    
    # Xóa các sản phẩm đã mua
    sort_index = np.delete(sort_index, liked_items)
    scores = np.delete(scores, liked_items)
    
    # sắp xếp và trả về theo số thứ tự của score
    arg_sort = np.argsort(-scores)
    
    # dùng sort_index để lấy số thứ tự ban đầu
    rmd_items = sort_index[arg_sort]
    
    if len(rmd_items) >= n_rmd_items and n_rmd_items is not None:
        rmd_items = rmd_items[: n_rmd_items]
    return rmd_items

def auc_score(predict_mat, bpr_mat):
    """
    Tính Area under the ROC curve (AUC)
    cho bài toán hệ khuyến nghị
    
    :param predict_mat: ma trận dữ đoán bpr mf
    :param bpr_mat: ma trận train hoặc test
    :return auc: area under the roc curve
    """
    auc = 0.0
    n_users, n_items = bpr_mat.shape
    
    # u và row tương ứng user và bp
    for u in range(n_users):
        y_pred = predict_mat[u]
        y_true = np.zeros(n_items)
        y_true[bpr_mat[u].indices] = 1
        auc += roc_auc_score(y_true, y_pred)
    auc /= n_users
    return auc

3.5 (SGD) thuật toán học BPR-MF

def learn_bpr_mf_sgd(bpr_mat, alpha=0.01, lamb=0.01, k=12, n_iters=10000):
    """
    Thuật toán học BPR MF SGD (một điểm dữ liệu duy nhất)
    
    :param bpr_mat: ma trận bpr
    :param alpha: hệ số learning rate
    :param lamb: hệ số lambda của bình thường hóa regularization
    :param k: số lượng latent factor trong bài toán MF
    :param n_iters: số vòng lặp
    
    :return W: ma trận W
    :return H: ma trận H
    """
    n_users, n_items = bpr_mat.shape
    # Khởi tạo ma trận W và ma trận H
    W = np.ones(shape=(n_users, k))
    H = np.ones(shape=(n_items, k))
    # Tập các sản phẩm nên khuyến nghị
    pos = np.split(bpr_mat.indices, bpr_mat.indptr)[1:-1]
    # Tập các sản phẩm không nên khuyến nghị
    neg = [np.setdiff1d(np.arange(0, n_items,1), e) for e in pos]
    
    # lặp
    for _ in range(n_iters):
        # ngẫu nghiên 3 bộ (u,i,j) từ D_S
        u = np.random.randint(0, n_users) 
        i = pos[u][np.random.randint(0, len(pos[u]))]
        j = neg[u][np.random.randint(0, len(neg[u]))]
        
        # Tính xuij
        xui = (W[u] * H[i]).sum()
        xuj = (W[u] * H[j]).sum()
        xuij = xui - xuj
        
        # mũ tự nhiên e của xuij
        exp_xuij = np.exp(xuij)
        
        # sgd cho tham số Theta (W và H)
        W[u] = W[u] + alpha * ( exp_xuij / (1+exp_xuij) * (H[i] - H[j]) + lamb * W[u])
        H[i] = H[i] + alpha * ( exp_xuij / (1+exp_xuij) * W[u] + lamb * H[i])
        H[j] = H[j] + alpha * ( exp_xuij / (1+exp_xuij) * (-W[u]) + lamb * H[j])
    return W, H

3.6 (Mini-Batch) thuật toán học BPR-MF

def learn_bpr_mf_mini_batch(bpr_mat, batch=100, alpha=0.01, lamb=0.01, k=12, n_iters=100):
    """
    Thuật toán học BPR MF Mini Batch
    
    :param bpr_mat: ma trận bpr
    :param batch: số lượng điểm dữ liệu mỗi n_iters
    :param alpha: hệ số learning rate
    :param lamb: hệ số lambda của bình thường hóa regularization
    :param k: số lượng latent factor trong bài toán MF
    :param n_iters: số vòng lặp
    
    :return W: ma trận W
    :return H: ma trận H
    """
    n_users, n_items = bpr_mat.shape
    # Khởi tạo ma trận W và ma trận H
    W = np.ones(shape=(n_users, k))
    H = np.ones(shape=(n_items, k))
    # Tập các sản phẩm nên khuyến nghị
    # (chuyển về numpy luôn cho tiện)
    pos = np.array(np.split(bpr_mat.indices, bpr_mat.indptr)[1:-1])
    # Tập các sản phẩm không nên khuyến nghị
    neg = np.array([np.setdiff1d(np.arange(0, n_items,1), e) for e in pos])
    
    # lặp
    for _ in range(n_iters):
        # mỗi u,i,j là một np array index
        u = np.random.choice(np.arange(0,n_users), batch, replace=False)
        i = []
        j = []
        for users in u:
            i.append(pos[users][np.random.randint(0, len(pos[users]))])
            j.append(neg[users][np.random.randint(0, len(neg[users]))])
        i = np.array(i)
        j = np.array(j)
        
        # Tính xuij
        xui = (W[u] * H[i]).sum(axis=1)
        xuj = (W[u] * H[j]).sum(axis=1)
        xuij = xui - xuj
        
        # mũ tự nhiên e của xuij
        exp_xuij = np.exp(xuij).reshape(batch, 1)

        # minibatch gradient descent cho Theta (W và H)
        W[u] = W[u] + alpha * ( exp_xuij / (1+exp_xuij) * (H[i] - H[j]) + lamb * W[u])
        H[i] = H[i] + alpha * ( exp_xuij / (1+exp_xuij) * W[u] + lamb * H[i])
        H[j] = H[j] + alpha * ( exp_xuij / (1+exp_xuij) * (-W[u]) + lamb * H[j])
    return W, H

3.7 Thử nghiệm

Thử nghiệm với phiên bản SGD (một điểm dữ liệu duy nhất):

W_sgd, H_sgd = learn_bpr_mf_sgd(bpr_train, n_iters=10000, k=12)
pred_mat_sgd = predict_bpr(W_sgd, H_sgd)

print('Train: %f' % auc_score(pred_mat_sgd, bpr_train))
print('Test: %f' % auc_score(pred_mat_sgd, bpr_test))

Train: 0.841916
Test: 0.828263

Thử nghiệm với phiên bản mini batch (batch=1000 điểm):

W_mb, H_mb = learn_bpr_mf_mini_batch(bpr_train, batch=100, n_iters=100, k=12)
pred_mat_mb = predict_bpr(W_mb, H_mb)

print('Train: %f' % auc_score(pred_mat_mb, bpr_train))
print('Test: %f' % auc_score(pred_mat_mb, bpr_test))

Train: 0.842083
Test: 0.829265

Trong trường hợp thực hành trên một tập dữ liệu khác, bạn có thể thử phiên bản mini-batch vì thường nó hoạt động ổn định hơn, ở đây mình muốn giữ nguyên tác bài báo nên thêm phiên bản sgd.

Để dự đoán danh sách những sản phẩm khuyến nghị cho người dùng $u$:

u = 28
n_rmd_items = 5
score = predict_bpr(W_mb, H_mb, u)
rmd_items = recommend_bpr(bpr_train, score, u, n_rmd_items)
print(rmd_items)

[257 287 180  99  49]

4. Phần kết

Github (chứa Jupyter Notebook): Tại đây

Trong bài viết này, ThetaLog giới thiệu những khó khăn của bài toán xây dựng hệ khuyến nghị từ thông tin phản hồi tiềm ẩn từ người dùng, đồng thời cài đặt thuật toán BPR-MF (Bayesian Personalized Ranking)!

Hy vọng bạn đọc sẽ có những giây phút thú vị với thuật toán!

ThetaLog - Nhật ký Theta

Lê Quang Tiến (quangtiencs)

Tham khảo

Steffen Rendle, Christoph Freudenthaler, Zeno Gantner and Lars Schmidt-Thieme. BPR: Bayesian Personalized Ranking from Implicit Feedback.
Weike Panand, Li Chen. GBPR: Group Preference Based Bayesian Personalized Ranking for One-Class Collaborative Filtering. Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence. https://www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/viewFile/6316/7124
Michael D. Ekstrand, Joseph A Konstan. Personalized Ranking (with Daniel Kluver). Matrix Factorization and Advanced Techniques - University of Minnesota. https://www.coursera.org/lecture/matrix-factorization/personalized-ranking-with-daniel-kluver-s3XJo
Kim Falk. Practical Recommender Systems. Manning Publications.
Ethen (MingYu) Liu. Bayesian Personalized Ranking. http://ethen8181.github.io/machine-learning/recsys/4_bpr.html
Alfredo Láinez Rodrigo, Luke de Oliveira. Distributed Bayesian Personalized Ranking in Spark. https://stanford.edu/~rezab/classes/cme323/S16/projects_reports/rodrigo_oliveira.pdf