PageRank và mối liên hệ xích Markov

Đăng trên bởi Lê Quang Tiến 19 phút trôi qua :D
Nội dung bài viết

PageRank là một thuật toán trước đây được Google Search sử dụng để xếp hạng trang web trên bộ máy tìm kiếm của họ. PageRank được lấy tên dựa trên đồng sáng lập Google - Larry Page.

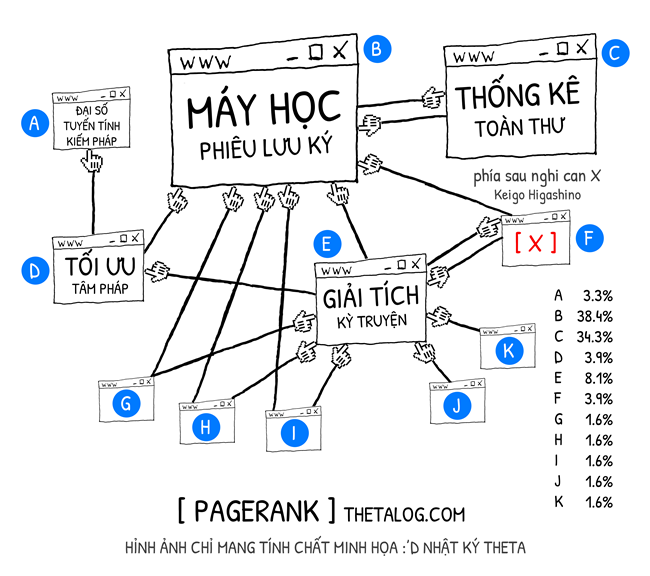
Thuật toán PageRank là một thuật toán học xếp hạng dựa trên phân tích đồ thị liên kết giữa các trang web, mỗi trang web sẽ được xem như một đỉnh, mỗi liên kết sẽ được xem như một cạnh của đồ thị.

Vì sao lại phân tích dựa trên liên kết giữa các trang web? Nếu xây dựng một thuật toán xử lý ngôn ngữ tự nhiên để xếp hạng các trang web thì có hợp lí hơn không? Nếu giải quyết theo hướng trên thì có lẽ bạn sẽ gặp hai vấn đề kha khá lớn đấy:

  • Tính toán không khả thi. Vào năm 1998, khi Google bắt đầu dịch vụ của mình họ phải đối mặt với $26$ triệu trang $(26 \times 10^{6})$, hai năm sau tức năm 2000 con số này là $1$ tỷ trang $(1 \times 10^{9})$… Tám năm sau, 2008 số lượng địa chỉ trang web khác nhau đạt $1$ nghìn tỷ $(1 \times 10^{12})$. Bài toán tìm kiếm là bài toán cần cập nhật kết quả càng sớm càng tốt, lượng truy xuất của người dùng lại cực lớn. Điều này dẫn đến chiến thuật thiết kế thuật toán dài hạn.
  • Văn hóa trích dẫn. Một số trang web nên được ưu tiên hơn, vì đó là trang nội dung nguồn. Những trang trích dẫn lại, hay nói cách khác sử dụng tài nguyên của trang nguồn thì phải ít ưu tiên hơn.

May mắn thay, có một cấu trúc đơn giản ở bên dưới mỗi trang web mà chúng ta có thể giải quyết vấn đề trên, các siêu liên kết (hyperlink) giữa các trang web!

Giả sử chúng ta có tập $n$ trang web được đánh số từ $1,…n$, PageRank của trang web $i$ được tính dựa trên các liên kết trang web khác đến nó (trang web $j$ liên kết trỏ đến $i$), nhưng không phải bất kì liên kết nào cũng cũng được tính điểm như nhau, chúng ta mong muốn một thuật toán thật công bằng! Thuật toán PageRank được xây dựng dựa trên hai ý tưởng cơ bản như sau:

  • Trang web $A$ trỏ liên kết đến $B$, nếu $A$ là một trang web xếp hạng cao trên bảng thì phải giúp $B$ có xếp hạng cao hơn.
  • Trang web $A$ trỏ liên kết đến $B$, lượng trang web mà $A$ trỏ tới nghịch biến với xếp hạng của $B$ hay nói cách khác $A$ trỏ đến càng nhiều trang thì giúp $B$ tăng thứ hạng càng ít.

Thuật toán PageRank giống như một lớp học nho nhỏ vậy vậy, khi đó giáo viên chính là thuật toán cuối cùng đánh giá lớp học đó, các bạn trong lớp viết ra tên những người bạn mà mình đánh giá cao kèm theo tên của mình. Kết quả cuối cùng công bố cho cả lớp công bằng nhất là khi:

  • Một bạn trong lớp được đánh giá cao, bạn ấy đánh giá cao một bạn khác trong lớp thì điều đó phải đáng tin cậy hơn một bạn khác ít được đánh giá cao hơn.
  • Một bạn đánh giá quá nhiều bạn thì có vẻ lập trường không vững, chúng ta sẽ giảm bớt một ít niềm tin vào những đánh giá này.

Tư tưởng thuật toán chỉ như vậy thôi, bây giờ chúng ta sẽ cùng bắt tay vào xây dựng thuật toán nhé!

1. Một ý tưởng chưa hoàn tất BadRank

Đặt $L_{i,j} = 1$ nếu như trang web $j$ có liên kết trỏ đến trang web $i$ (kí hiệu $j \rightarrow i$), ngược lại $L_{i,j} = 0$.

Lúc này ta có $m_{i} = \sum_{k=1}^{n} L_{k,j}$ là tổng số liên kết mà web $j$ trỏ đến các trang web khác.

Với hai ý tưởng xây dựng thuật toán được nêu trên, chúng ta có thể “tạm” định nghĩa độ đo $BadRank$ như sau:

$$p_{i} = \sum_{j \rightarrow i} \frac{p_{j}}{m_{j}} = \sum_{j=1}^{n} \frac{L_{i,j}}{m_{j}} p_{j} $$

Công thức trên thỏa mãn hai ý tưởng về thuật toán mà chúng ta đã bàn:

  • Nó đồng biến với $p_{j}$: hay nói cách khác nếu như trang web $j$ là một trang web nổi tiếng và có liên kết đến với $i$ thì sẽ tăng mức ảnh hưởng của $i$.
  • Nghịch biến với $m_{j}$: hay nói cách khác nếu như trang web $j$ có quá nhiều liên kết tới các trang web khác thì uy tín mà $j$ đóng góp cho $i$ càng ít.

Để tiện cho việc tính toán chúng ta sẽ định nghĩa công thức trên dưới dạng ma trận.

Gọi $\mathbf{p}$, $\mathbf{L}$, $\mathbf{M}$ lần lượt là các ma trận $n \times 1$, $n \times n$, $n \times n$ lưu giữ thông tin của $p_{i}$, $L_{i,j}$, $m_{i}$ như sau:

$$\mathbf{p} = \left[ {\begin{array}{*{20}{c}} p_{1} \\ p_{2} \\ \vdots \\ p_{3} \end{array}} \right]$$

$$\mathbf{L} = \left[ {\begin{array}{*{20}{c}} L_{1,1} & L_{1,2} & \cdots & L_{1,n} \\ L_{2,1} & L_{2,2} & \cdots & L_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ L_{n,1} & L_{n,2} & \cdots & L_{n,n} \end{array}} \right]$$

$$\mathbf{M} = \left[ {\begin{array}{*{20}{c}} m_{1} & 0 & \cdots & 0 \\ 0 & m_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & m_{n} \end{array}} \right]$$

Viết lại dưới dạng ma trận: $\mathbf{p} = \mathbf{L} \mathbf{M}^{-1} \mathbf{p}$, nếu như đặt $\mathbf{A} = \mathbf{L} \mathbf{M}^{-1}$ ta có $\mathbf{p} = \mathbf{A} \mathbf{p}$.

Đến đây có lẽ bạn đã nhận ra $\mathbf{p}$ chính là vector riêng của $\mathbf{A}$ với trị riêng $1$, $\mathbf{A}$ lại là ma trận thưa (sparse matrix - vì $\mathbf{L}$ là ma trận thưa, một trang web chỉ liên kết với một số ít trang web trên không gian mạng thôi). Mà chúng ta lại biết rằng có một số phương pháp tính hiệu quả dành riêng cho bài toán trị riêng - vector riêng trên ma trận thưa nữa! Nghe thật tuyệt vời phải không nào!

Tôi sung sướng. Nhưng vội vàng một nửa… Trong giây phút ấy, bạn chợt nhận ra hai vấn đề, nếu phân tích kỹ, đây là hai câu hỏi buộc chúng ta phải trả lời:

  • Thứ nhất: Liệu rằng $\mathbf{A}$ thực sự có trị riêng $1$.
  • Thứ hai: Và giả định nếu như $\mathbf{A}$ có trị riêng là $1$ đi, liệu $\mathbf{p}$ có rơi vào một trường hợp đặc biệt nào đó mà kết quả chẳng có ý nghĩa gì với chúng ta không? Một trị riêng có thể có nhiều vector riêng, liệu $\mathbf{p}$ là nghiệm duy nhất mà ta tìm được?

Ít nhất có 2 trường hợp của các loại đồ thị mà việc lấy vector riêng của bài toán này không mang lại kết quả chúng ta mong muốn:

  • Đồ thị không liên thông: nhiều hơn một vector riêng.
  • Đồ thị chứa đỉnh đu đưa: những đỉnh không trỏ liên kết về bất kì trang web nào dù có liên kết trang web khác trỏ tới.

Thử một ví dụ nhé, ví dụ còn lại bạn đọc tự thực hiện.

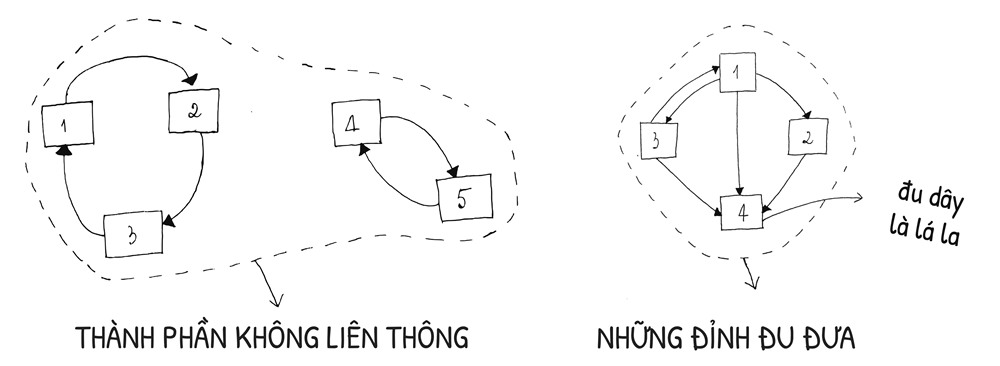
Trường hợp “thành phần không liên thông” của đồ thị trên:

  • Ta có: $\mathbf{A} = \left[ {\begin{array}{*{20}{c}} 0 & 0 & 1 & 0 &0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \end{array}} \right] $

  • Với trị riêng là $1$ chúng ta có hai vector riêng

$$\mathbf{p} = \left[ {\begin{array}{*{20}{c}} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 & 0 \end{array}} \right]^{\intercal}$$

$$\mathbf{p} = \left[ {\begin{array}{*{20}{c}} 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \end{array}} \right]^{\intercal}$$

Hai kết quả là hai kết quả đối lập nhau! Nếu như giả sử rằng hai trị riêng “hao hao nhau” thì chúng ta có thể sắp xếp và chọn, tuy nhiên chúng lại hoàn toàn trái ngược nhau, chúng ta từ chối đây là một lời giải hợp lí! Ví dụ cạnh bên thì bạn sẽ không tìm được bất kì trị riêng nào bằng $1$, giải thử nhé!

Từ những câu hỏi trên chúng ta sẽ đi tìm câu trả lời… để hiểu bài toán chúng ta sẽ cùng nhau tìm hiểu về xích Markov, phân bố dừng, điều kiện tồn tại phân bố dừng và cuối cùng là chìa khóa lời giải cuối cùng của thuật toán PageRank!

2. Xích Markov và phân bố dừng

2.1 Xích Markov hữu hạn trạng thái đồng nhất thời gian

Xích Markov là một mô hình toán học mô tả quá trình chuyển dịch từ một trạng thái sang một trạng thái khác dựa trên một số quy luật xác suất nhất định. Trong một quá trình như vậy, xích Markov không quan tâm đến thông tin quá trình bằng cách nào ta chuyển dịch đến trạng thái hiện tại, xác suất của trạng thái tiếp theo phụ thuộc vào trạng thái hiện tại và thông tin xác suất đang có tại thời điểm $t$.

Nếu giả định rằng biến ngẫu nhiên trạng thái quan sát được là biến ngẫu nhiên rời rạc, hay $X_{t} \in \{1,…,k\}$ trạng thái, lúc này mô hình của chúng ta là xích Markov hữu hạn trạng thái (finite-state Markov chain). Xác suất có điều kiện chuyển dịch khi biết trạng thái hiện tại $\Pr(X_{t} | X_{t-1})$ có thể viết lại dưới dạng ma trận $k \times k$, được gọi là ma trận chuyển dịch $P$, với $P_{i,j} = \Pr(X_{t} = j | X_{t-1} = i)$ là xác suất chuyển dịch từ trạng thái $i$ sang trạng thái $j$. Mỗi hàng của ma trận $P$ có tổng $\sum_{j} P_{i,j} = 1$, vì vậy ma trận này được gọi là ma trận ngẫu nhiên (stochastic matrix).

Khi mà ma trận chuyển dịch độc lập với thời gian, nghĩa là quá khứ, hiện tại, tương lai chúng ta chỉ có duy nhất một ma trận chuyển dịch thôi hay nói cách khác $\Pr(X_{t+1} =x | X_{t} =y) = \Pr(X_{t} =x | X_{t-1} =y)$ chúng ta gọi đây là một xích Markov đồng nhất thời gian (time-homogeneous Markov chains).

Bạn có thể tưởng tượng một xích Markov hữu hạn đồng nhất thời gian như một cỗ máy đặc biệt vậy, hãy tưởng tượng về một hệ động lực ngẫu nhiên… Hãy tưởng tượng mỗi quả banh sẽ thay đổi trạng thái trong hệ thông qua những chiếc máy bơm ngẫu nhiên… Tại mỗi thời điểm $t$ sang $t+1$ máy bơm sẽ bắn các quả banh theo những đường ống với xác suất nhất định.

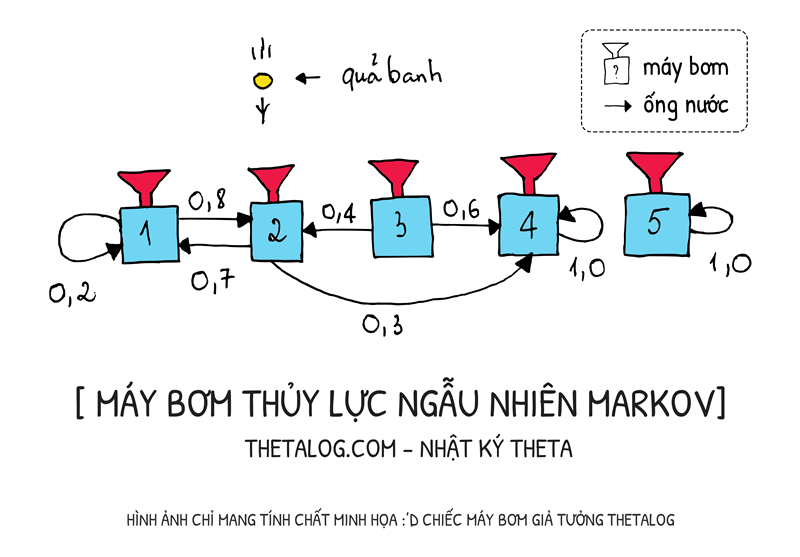
Trong hình trên, nếu quả banh đang ở máy bơm thứ $2$ tại thời điểm $t=1$, tại thời điểm $t=2$ quả banh sẽ được bắn đi sang một máy bơm khác, có thể là máy bơm $1$ hoặc cũng có thể là máy bơm $2$.

Ma trận chuyển dịch xác suất của xích Markov hữu hạn đồng nhất thời gian trên có thể viết lại như sau:

$$P = \left[ {\begin{array}{*{20}{c}} 0,2 & 0,8 & 0 & 0 &0 \\ 0,7 & 0 & 0 & 0,3 & 0 \\ 0 & 0,4 & 0 & 0,6 & 0 \\ 0 & 0 & 0 & 1,0 & 0 \\ 0 & 0 & 0 & 0 & 1,0 \end{array}} \right]$$

Viết dưới dạng ma trận sẽ giúp chúng ta tiện lợi hơn trong việc biểu diễn quá trình trong hệ. Giả sử như chúng ta có một vector cột $\pi^{(1)}$ (kích thước $k \times 1$) thể hiện phân bố đầu vào. Giả sử có $1000$ quả banh, số banh mà chúng ta thả vào các trạng thái $1,2,3,4,5$ lần lượt là $400,300,100,120,80$. Chúng ta có vector phân bố ban đầu $\pi^{(1)} = \left[ {\begin{array}{*{20}{c}} 0,4 & 0,3 & 0,1 & 0,12 & 0,08 \end{array}} \right]^{\intercal} $. Câu hỏi được đặt ra là phân bố tại thời gian $t+1$ sẽ là bao nhiêu? Rất đơn giản:

$$\pi^{(2)} = P^{\intercal} \pi^{(1)}$$

Hay nói cách khác, lúc này $\forall i$ ta có $\pi^{(t+1)}_{i} = \sum_{k} \pi^{(t)}_{k} \cdot P_{k,i} = \sum_{k} \pi^{(t)}_{k} \cdot \Pr(X_{t+1} = i | X_{t} = k)$ được hiểu như là tổng tỷ lệ chuyển từ trạng thái khác đến và tỷ lệ giữ lại ở trạng thái gốc.

2.2 Phân bố dừng

Hệ mà chúng ta đang xét là một xích Markov hữu hạn đồng nhất thời gian. Hãy tưởng tượng mỗi quả banh sẽ thay đổi trạng thái trong hệ thông qua những chiếc máy bơm ngẫu nhiên. Giờ hãy mang thật nhiều quả banh thả đồng loạt vào hệ.

Lặp đi lặp lại quá trình xảy ra trong hệ:

$$\pi^{(t+1)} = P^{\intercal} \pi^{(t)}$$

Liệu tồn tại một trạng thái nào đó, tại đó những chiếc máy bơm ngẫu nhiên vẫn hoạt động ngày đêm nhưng phân bố trạng thái hệ đứng yên? Nghĩa là, tồn tại một phân bố đặc biệt, mà ở đó nếu như hệ chạm đến thì sẽ không thoát được phân bố này:

$$\pi = P^{\intercal} \pi$$

(lưu ý: nhiều tài liệu viết $\pi$ dưới dạng vector dòng, ThetaLog chọn cách biểu diễn vector cột)

Người ta gọi đây là trạng thái cân bằng (equilibrium), và phân bố lúc này là phân bố dừng (stationary distribution) của xích Markov hữu hạn đồng nhất thời gian.

Nếu nhìn kỹ bạn sẽ thấy đây là bài toán trị riêng, vector riêng của ma trận $P^{\intercal}$ với trị riêng $\lambda = 1$. Như chúng ta đã biết về bài toán trị riêng, vector riêng là một trị riêng $\lambda$ có thể có rất nhiều vector riêng, hơn nữa $P^{\intercal}$ chưa chắc có trị riêng $\lambda = 1$, bài toán trở nên rối rắm!

May mắn thay, có một định lý trong đại số tuyến tính giúp chúng ta có thể trả lời câu hỏi trên.

Định lý Perron Frobenius
Nếu như ma trận ngẫu nhiên cột (tổng thành phần từng cột bằng $1$) mà ta đang xét $M$ là ma trận dương có từng thành phần $M_{i,j} > 0$ thì ma trận $M$ chỉ có duy nhất một phân bố dừng (duy nhất một vector riêng tương ứng trị riêng $1$). Tất cả trị riêng còn lại nhỏ hơn $1$.

TL;DR: phần chứng minh định lý sẽ không được bàn ở đây, bạn đọc quan tâm có thể đọc thêm tài liệu đính kèm. [Ref 7 (ghi chú 33-34), 8]

Định lý Perron Frobenius chỉ ra rõ những ma trận thỏa điều kiện trên thì sẽ chắc chắn có trị riêng là $1$ và duy nhất một vector riêng ứng với $1$. Phải chăng đây là mảnh ghép cuối cùng của bài toán!

3. Thuật toán PageRank

3.1 Diễn giải BadRank dưới dạng xích Markov

Mỗi trang web có thể xem như một trạng thái. Tại mỗi trang web $i$ có $m_{i}$ liên kết khác nhau, xem xác suất mà chúng ta chuyển sang trang web khác là đồng nhất hay nói cách khác xác suất chuyển sang trang web khác là $1 / m_{i}$. Giờ chúng ta có thể diễn giải BadRank dưới dạng xích Markov hữu hạn trạng thái đồng nhất thời gian:

  • Ma trận chuyển dịch: $P = A^{\intercal}$
  • Xác suất chuyển dịch trạng thái: $\Pr(X_{t+1} = j | X_{t} = i) = 1 / m_{i}$ nếu có liên kết từ $i$ sang $j$, ngược lại $\Pr(X_{t+1} = j | X_{t} = i) = 0$

Người dùng như những “quả banh” trong hệ thống động lực ngẫu nhiên ban đầu vậy, lướt web ngẫu nhiên dựa trên những liên kết. Liệu có tồn tại phân bố dừng? Trang web nào có tỷ lệ người xem nhiều nhất?

3.2 Thuật toán PageRank

Thuật toán PageRank chỉnh sửa nho nhỏ lại ý tưởng ban đầu, bằng cách thêm một tham số $d$ (được gọi là Damping Factor) để “làm mềm” lại bài toán ban đầu:

  • Nếu có liên kết từ $j$ đến $i$: $p_{i} = \frac{1-d}{n} + \frac{d}{m_{j}}$
  • Ngược lại: $p_{i} = \frac{1-d}{n}$

Với $0 < d < 1 $, Google sử dụng $d=0,85$. Nếu viết lại dưới dạng ma trận chúng ta có thể phát biểu thuật toán PageRank như sau:

Thuật toán PageRank
Tìm vector $\mathbf{p}$ thỏa mãn:$$\mathbf{p} = \left( \frac{1-d}{n} E + d \mathbf{L} \mathbf{M}^{-1} \right) \mathbf{p} $$Với $E$ là ma trận $n \times n$ trang web tất cả phần tử bằng $1$.

Mô hình mới có thể diễn giải như sau, những người lướt web ngẫu nhiên trên những liên kết ban đầu, tuy nhiên một lúc sau thì họ cảm giác “chán với những trang web hao hao nhau” và đột ngột nhảy sang khác không liên quan gì đến liên kết đầu cả.

Nếu bạn chú ý kỹ sẽ thấy những trường hợp như đồ thị không liên thông hay tồn tại những đỉnh đu đưa là trường hợp đặc biệt của ma trận có chứa phần tử $0$. Việc thêm ma trận $E$ vào nhằm giải quyết vấn đề có phân bố dừng hay không.

Hợp lí không? Hợp lí chứ! Và tất nhiên sẽ còn hợp lí hơn nữa vì định lý Perron Frobenius cho chúng ta biết rằng để giải được bài toán này, điều cần thiết đầu tiên là phải “làm mất mấy số $0$ trong ma trận ban đầu đi”, việc thêm ma trận $E$ với hệ số $d$ tác dụng cốt lõi là làm việc này!

3.3 Phương pháp tính

Nếu như cài đặt thuật toán PageRank để tìm vector $\mathbf{p}$ dựa trên các phương pháp truyền thống, dùng các thư viện đại số tuyến tính, bình thường sẽ mất khoảng $n^{3}$ phép toán… Hơn nữa số lượng trang web $n$ lại rất lớn, việc lưu trữ bộ nhớ nên tiết kiệm tối đa.

Phương pháp để tính toán hiệu quả thường dùng cho bài toán này là Power iteration. Power iteration thường được áp dụng cho các ma trận lớn khi mà chúng ta chỉ đi tìm duy nhất một vector riêng, tư tưởng thuật toán rất đơn giản lặp đến khi chạm đến phân bố dừng:

  • Khởi tạo một vector phân bố $\mathbf{p}^{(0)}$ bất kì.
  • Tính ma trận ngẫu nhiên cột Google: $\mathbf{G} = \frac{1-d}{n} E + d \mathbf{L} \mathbf{M}^{-1}$
  • Lặp đến khi hội tụ: $\mathbf{p}^{(t+1)} = \mathbf{G} \mathbf{p}^{(t)}$
#   _______________________________________________________________________
#  |[] ThetaLogShell                                                 |X]|!"|
#  |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
#  | > ThetaLog.com                                                      | |
#  | > ENV: Python 3.6.5 Anaconda                                        | |
#  | > PageRank                                                          | |
#  |_____________________________________________________________________|/

import numpy as np

def pagerank(A, epsilon=1.0e-8, d=0.85):
    """
    Thuật toán đánh giá PageRank

    :param A: numpy.ndarray - ma trận N rows N cols
    :param epsilon: float - epsilon càng nhỏ độ chính xác càng lớn
    :param d: float - damping factor của PageRank

    :return p: numpy.ndarray - vector đánh giá N rows 1 col (càng cao thì xếp hạng càng cao)
    """
    # Lấy kích thước ma trận vuông a (hoặc N = A.shape[1])
    N = len(A)

    # khởi tạo p vị trí ban đầu ngẫu nhiên và một vector ngẫu nhiên khác
    # để kiểm soát hội tụ của vector p
    p = np.random.dirichlet(np.ones(N),size=1).reshape(N,1)
    last_p = np.random.dirichlet(np.ones(N),size=1).reshape(N,1)
    
    # tính ma trận G
    G = (1 - d) / float(N) * np.ones((N, N), dtype=np.float32) + d * A 
    
    # Lặp đến khi hội tụ
    while np.linalg.norm(p - last_p, 2) > epsilon:
        last_p = p
        p = G @ p

    # Trả về kết quả
    return p

Chạy thử thuật toán:

# Ma trận ngẫu nhiên cột A
A = np.array([[0, 0, 0, 0, 1],
              [0.5, 0, 0, 0, 0],
              [0.5, 0, 0, 0, 0],
              [0, 1, 0.5, 0, 0],
              [0, 0, 0.5, 1, 0]])

# Chạy thuật toán
p = pagerank(A, epsilon=1.0e-8, d=0.85)

Tuy nhiên đây cũng không hẳn là phương pháp tối ưu nhất, nếu bạn đọc quan tâm có thể tìm hiểu về Monte Carlo power method để tính toán song song trên hệ thống phân tán, ngoài ra một số vấn đề về tính toán trên ma trận thưa cũng hữu ích không kém!

4. Web spam - tiêu cực bên ngoài hệ thống

Nếu bạn có ý định dùng thuật toán này để đánh giá sản phẩm thì không sao cả, đây là một thuật toán rất tốt. Tuy nhiên hãy cẩn thận nếu như bạn dùng thuật toán này cho công cụ tìm kiếm khi dữ liệu phát sinh từ một nguồn khác.

PageRank và các biến thể của nó được Google sử dụng rất lâu cho đến khi một vài vấn đề xảy ra. Thời báo New York vào 2011 có bài báo nổi tiếng sau: Search Optimization and Its Dirty Little Secrets

Trang web JC Penney đứng đầu trên rất nhiều chủ đề tìm kiếm của Google! Thật khó tin, bằng cách nào nhỉ?

Thuật toán PageRank không dể sử dụng, rất dể bị ảnh hưởng tiêu cực bởi việc các trang web spam liên kết lẫn nhau, bởi vì nguồn dữ liệu phát sinh từ các bộ crawler phân tích tự động. Như bạn đã biết việc thêm $d$ (Damping Factor) vào hệ thống sẽ làm tất cả các trang web đều có mức ảnh hưởng nhất định. Hãy nghĩ đến việc bạn có $1000, 2000,…$ trang web, và bạn quyết định sử dụng chúng để tăng hạng tìm kiếm cho một trang nào đó! Mấu chốt là ở phần xây dựng thuật toán, dù biết là mỗi một trang có sức ảnh hưởng rất nhỏ nhưng khi cộng dồn lại thì sức ảnh hưởng nó rất lớn!

Giới doanh nghiệp thì họ gọi đây là tối ưu tìm kiếm Search engine optimization (SEO) nhưng đối với các công ty tìm kiếm thì họ sẽ gọi đây là Web spam. Hãy cẩn thận khi sử dụng thuật toán, tránh hệ thống bị tiêu cực, nếu bạn là người làm sản phẩm và mong muốn người dùng mình luôn hưởng chất lượng dịch vụ tốt nhất!

5. Phần kết

Thuật toán PageRank là thuật học để đánh giá các đỉnh của một đồ thị có hướng dựa trên mức độ quan trọng của chúng. Về cơ bản, kết quả của thuật toán PageRank dựa trên việc tìm phân bố dừng của một xích Markov hữu hạn đồng nhất thời gian. Để tồn tại lời giải phân bố dừng cho bài toán chúng ta thêm hệ số Damping Factor để thỏa định lý Perron Frobenius và giả định rằng người dùng lướt web ngẫu nhiên.

Thuật toán PageRank không chỉ dùng cho các bộ tìm kiếm, thuật toán PageRank được sử dụng rộng rãi trong các bài toán Graph Mining như sinh học, hóa học, các bài toán khoa học xã hội, vật lý,…

Chúc bạn có những ứng dụng thú vị với PageRank!

Tham khảo

  1. Trevor Hastie, Robert Tibshirani, Jerome Friedman. The Elements of Statistical Learning Data Mining, Inference, and Prediction (chapter 14.10). Springer. 2017.
  2. Ryan Tibshirani. PageRank - Data Mining: Spring 2013. January 22 2013. http://www.stat.cmu.edu/~ryantibs/datamining/
  3. Wikipedia contributors. “PageRank.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 9 Sep. 2018. Web. 10 Sep. 2018.
  4. Google Blog. We knew the web was big… July 25, 2008. https://googleblog.blogspot.com/2008/07/we-knew-web-was-big.html
  5. Dustin Stansbury. A Brief Introduction to Markov Chains. https://theclevermachine.wordpress.com/tag/time-homogeneous-markov-chain/
  6. Jeremykun. Google’s Page Rank – Why it Doesn’t Work Anymore. June 21, 2011. https://jeremykun.com/2011/06/21/googles-page-rank-why-it-doesnt-work-anymore/
  7. Oliver Knill. Math 19b, Linear Algebra, Probability and Statistics, Spring, 2011. http://www.math.harvard.edu/~knill/teaching/math19b_2011/handouts.html
  8. Shlomo Sternberg. Dynamical Systems. http://www.math.harvard.edu/library/sternberg/slides/1180912pf.pdf