Normalizing Flows và giới thiệu RealNVP
Nội dung bài viết
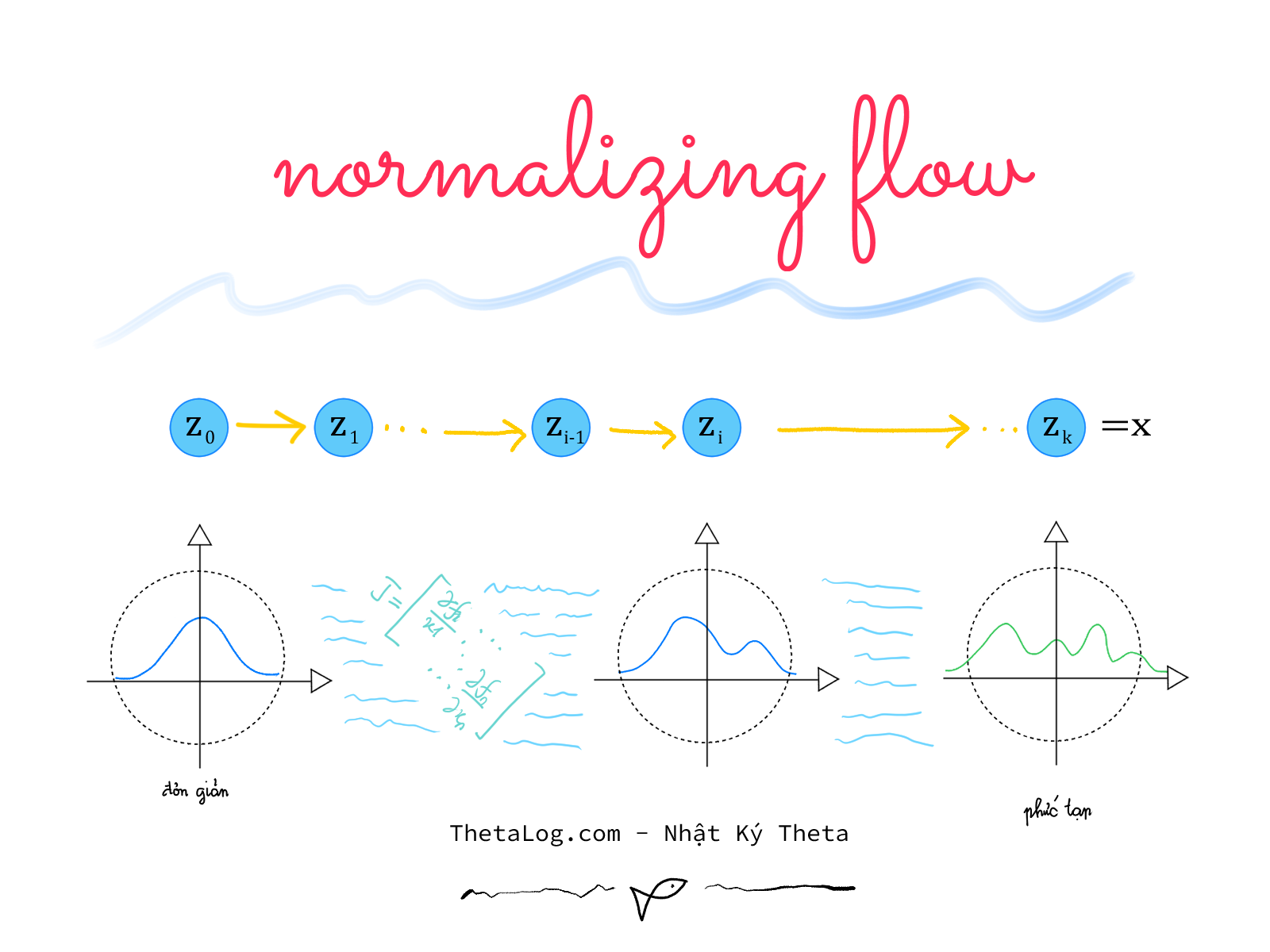
Normalizing Flows là nhóm mô hình sinh (generative models) mô hình hóa các phân bố phức tạp bằng cách sử dụng kỹ thuật đổi biến thông qua việc xây dựng các phép biến đổi khả nghịch phức tạp, linh hoạt. Trong bài viết này chúng ta sẽ tìm hiểu Normalizing Flows và một mô hình nổi tiếng khá phổ biến RealNVP.
Thế giới xác suất đắm chìm trong việc mô hình hóa tính chắc chắn của các sự kiện thông qua bản đồ niềm tin đặc tả bởi các con số, được xây dựng bởi các nhà toán học qua các phân bố xác suất.
Nhiều ứng dụng thú vị có thể xây dựng trên việc tính toán các phân bố xác suất phức tạp.
Ấy thế, thế giới thì quá đỗi tinh vi, phức tạp, rối rắm, khó lòng có thể mô hình hóa qua vài dòng công thức đơn giản mà quán triệt được hết vũ điệu hỗn độn và hài hòa của không gian sự kiện.
Hẳn vẫn có những trường hợp ta có thể xây dựng mô hình gần đúng và hữu dụng, như là người ta có thể mô hình hóa số lượng xe đi ngang qua một điểm trên con đường trong một khoảng thời gian cho trước với phân bố possion, hay mô hình hóa thời gian cho đến khi bạn bị tai nạn giao thông lần nữa với phân bố mũ,… Khi được sắp xếp một trình tự sự kiện xuất hiện hợp lý chúng ta sẽ có mô hình xác suất thống kê, các mô hình này có thể điều chỉnh sao cho gần với thực tế qua các tập tham số.
Tuy nhiên vẫn có những vấn đề hết sức phức tạp, chẳng hạn như ảnh số, một bức ảnh số trắng đen thông thường cũng đã hẳn chứa $1920 \times 1080 = 2,073,600$ điểm ảnh hay $2.0$ MegaPixels, số lượng điểm ảnh đủ khổng lồ để dù một bộ óc thông thái siêu phàm cũng khó lòng viết ra công thức tường minh phân bố sinh ra ảnh khuôn mặt người mà có thể dừng bút đặt dấu chấm hết gói gọn trong vài trang giấy.
Tính toán, thao tác các phép toán trên phân bố phức tạp cũng rất khó khăn đầy thách thức. Một trong mẹo giải toán thú vị là chuyển bài toán khó thành bài toán dể hơn, liệu có cách nào giúp chúng ta chuyển phân bố phức tạp $D$ chiều thành một phân bố đơn giản $D$ chiều, khi mà phân bố đơn giản $D$ chiều chúng ta quá rạch ròi việc tính toán, việc tính toán phân bố phức tạp sẽ thông qua việc biến đổi kết quả từ phân bố đơn giản?
Normalizing Flows là một công cụ như thế, lấy ý tưởng chủ đạo của công thức đổi biến (change variable formula) biến đổi phân bố phức tạp thành phân bố đơn giản qua các phép biển đổi khả nghịch…
1. Mảnh ghép đầu tiên - công thức đổi biến:
1.1 Một ví dụ đơn giản minh họa:
Trong một đêm mưa gió giông bão, câu chuyện bắt đầu bằng mấy thí nghiệm và giả định vu vơ…
Giả sử ta có một biến ngẫu nhiên liên tục $\color{#007aff} z$ biết trước hàm mật độ p.d.f, $\color{#007aff} z$ có phân bố đều nằm trên giá $[1, 3]$ hay $\color{#007aff} z \color{black} \sim \mathcal{U}([1,3])$.
Gọi $\color{#34c759} x$ là một biến ngẫu nhiên chưa biết hàm mật độ nhưng biết phép biến đổi $g(z)=\frac{1}{40} z^4 + \frac{39}{40}$ đơn điệu nghiêm ngặt trên $[1, 3]$, biến đổi $\color{#007aff} z$ thành $\color{#34c759} x$ hay $x=g(z)$.
Mật độ điểm đã có sự thay đổi. Số lượng điểm trong khoảng $\color{#007aff} [1.0, 1.1]$ nay đã không tương ứng với $\color{#34c759} [1.0, 1.1]$ nữa, hiển nhiên, giờ đây số lượng điểm $\color{#007aff} [1.0, 1.1]$ tương ứng với $\color{#34c759} [g(1.0), g(1.1)] = [1.0, 1.0116025]$ nếu ta phóng to và đếm từng điểm một.
Bảo toàn! Bạn chợt nhận ra, mọi thứ chẳng biến mất đi đâu cả, chỉ có mật độ là thay đổi. Thứ biểu diễn cho mật độ nhiều ít của một biến ngẫu nhiên liên tục là hàm mật độ. Thứ biểu diễn cho cơ hội của biến ngẫu nhiên xảy ra là phần diện tích tương ứng cho từng đoạn của biến ngẫu nhiên ấy.
Nói thế, thì vẫn chưa giải quyết được gì cả. Thế là ta lại viết suy nghĩ ấy ra dưới dạng công thức tường minh, phần diện tích ban đầu tương ứng với phần diện tích biến đổi có thể viết (và thêm vì tính đơn điệu nghiêm ngặt, mới viết được vầy):
$$\color{#007aff} |p_z(z)dz| \color{black} = \color{#34c759} | p_x (g(z)) dg(z)|$$
Hay:
$$\color{#007aff} |p_z(z)dz| \color{black} = \color{#34c759} | p_x (x) dx|$$
Một tí vẽ vời cho dể hình dung nào… (đáng lẽ ở đây phần diện tích sẽ rất nhỏ, tuy nhiên để dể hình dung thì ta chọn một đoạn lớn nhé):
Biến đổi tương đương ta có:
$$\begin{array}{*{20}{l}} \color{#34c759} p_x (x) & = & \color{#007aff} p_z(z) \color{black} \left| \frac{dz}{dx} \right| \\ & = & \color{#007aff} p_z(z) \color{black} \left| \frac{dx}{dz} \right|^{-1} \\ & = & \color{#007aff} p_z(z) \color{black} \left| \frac{dg(z)}{dz} \right|^{-1} \\ & = & \color{#007aff} p_z(z) \color{black} \left| g’(z) \right|^{-1} \end{array}$$
Do đó:
$$ \color{black} p_x (x) = p_z(g^{-1}(x)) \left| g’(g^{-1}(x)) \right|^{-1}$$
Công thức trên được gọi là công thức đổi biến cho phép chúng ta tìm được hàm mật độ $\text{p.d.f}$ của biến ngẫu nhiên liên tục chưa biết $x$, khi biết hàm mật độ $p_z(z)$, phép biến đổi $x=g(z)$ và hàm nghịch đảo $g^{-1}$ tương ứng của $g$.
Bài tập: thử thế $g$ vào công thức trên. Và vẽ thử ra hàm mật độ, xem có giống kết quả xấp xĩ hàm mật độ khi ta lấy mẫu không?
1.2 Công thức đổi biến cho vectơ ngẫu nhiên
Phần công thức sau cho vectơ ngẫu nhiên tạm thời sẽ không chứng minh. Bạn đọc quan tâm có thể tìm các tài liệu liên quan. Tuy nhiên hãy cẩn thận với tính đơn điệu trong phép biến đổi, tạm thời giản lược phần này, bạn đọc quan tâm sâu hơn về điều kiện cần của công thức này có thể tự tìm hiểu thêm…
| Công thức đổi biến cho vectơ ngẫu nhiên (Change of Variables Formula - Probability Topic) |
|---|
Gọi $\mathbf{x} = [x_1,..., x_D ]^{\intercal} \in \mathbb{R}^{D}$ và $\mathbf{z} = [z_1,..., z_D ]^{\intercal} \in \mathbb{R}^{D}$ là hai vectơ ngẫu nhiên liên tục $D$ chiều với $\mathbf{x}=g(\mathbf{z})$. Công thức đổi biến cho ta biết hàm mật độ chưa biết $p_{\mathbf{x}}$ khi biết $p_{\mathbf{z}}$ và $g^{-1}$:
$$ p_{\mathbf{x}}(\mathbf{x}) = p_{\mathbf{z}} (g^{-1} (\mathbf{x})) \left| \text{det} \left( \frac{\partial g^{-1} (\mathbf{x}) }{ \partial \mathbf{x} }\right) \right|$$ Ghi chú:
|
2. Mảnh ghép thứ hai - luồng khả nghịch:
Giờ đây ta như đứa trẻ, khám phá ra đôi điều hay ho như nhặt được mảnh vỏ sò ở bãi biển. Nhưng để rồi lại nhận thấy thế giới còn quá lớn và nhiều điều chưa biết…
Trong trường hợp trên, ta biết trước $g$ và tính toán được $g’$, $g^{-1}$, tuy nhiên trong trường hợp thực tế thì $g$ nào đâu có biết.
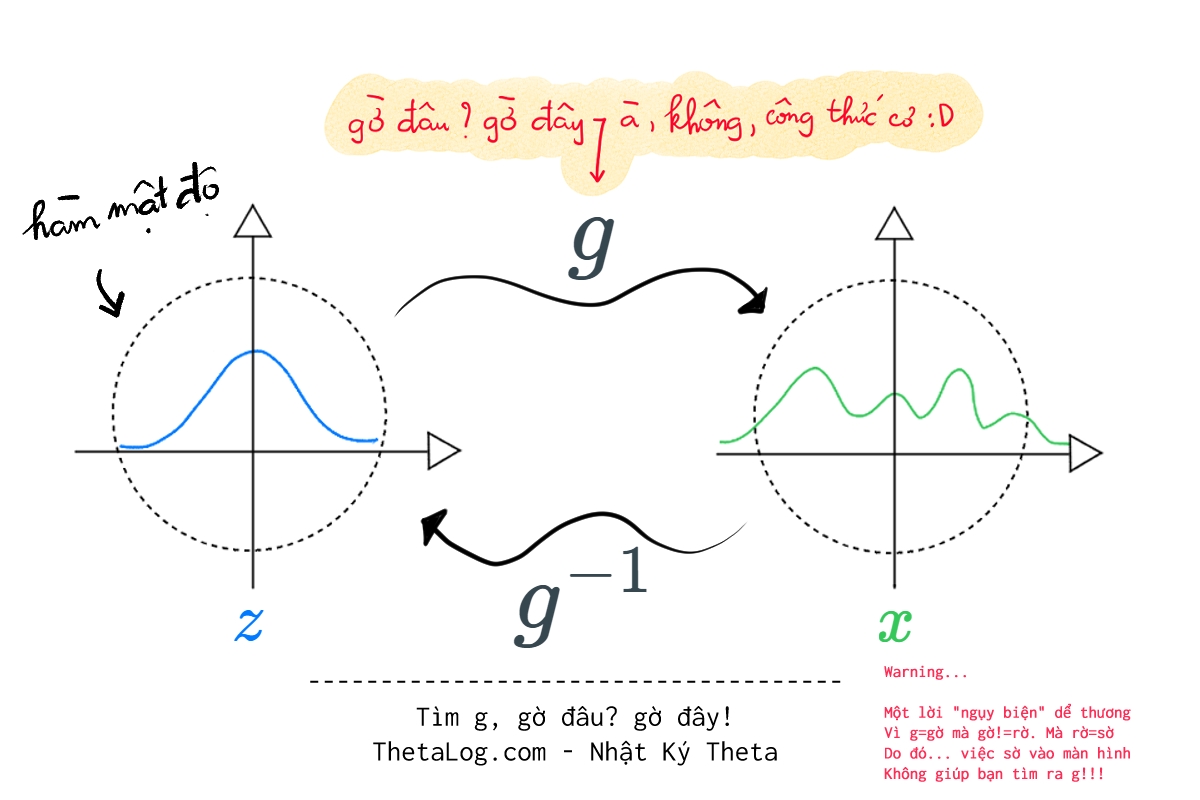
Thế ta lại mày mò việc mô hình hóa $g$, liệu có cách nào xây dựng một $g$ linh hoạt ứng biến cho nhiều trường hợp khác nhau. Nhận ra:
1) Trước hết, một hàm khả nghịch $g$ có thể tham số hóa, tham số này có thể học được, nhờ đó sẽ linh động trong nhiều tình huống.
2) Thêm nữa, một hàm khả nghịch $g$ có thể xem như là một hàm hợp lồng nhau của nhiều hàm khả nghịch. Do tính chất đặc biệt hàm hợp, nếu $g =g_1 \circ g_2 \circ g_3$ hay $g(x) = g_1(g_2(g_3(x))) = (g_1 \circ g_2 \circ g_3)(x)$ nếu muốn tìm hàm nghịch $g^{-1} = g_3^{-1} \circ g_2^{-1} \circ g_1^{-1}$. Quá thuận lợi! Trong trường hợp tổng quát, nếu $g = g_1 \circ … \circ g_K$ thì $g^{-1} = g_K^{-1} \circ … \circ g_1^{-1}$.
3. Normalizing Flow
Normalizing Flow là sự kết hợp hai mảnh ghép ý tưởng (1) đổi biến (2) dùng luồng các phép biến đổi khả nghịch được tham số hóa và học từ dữ liệu để biến đổi phân bố đơn giản thành phân bố phức tạp, nhờ đó ta có thể tính toán xác suất trên hàm mật độ như lấy mẫu hoặc định lượng chắc chắn.
- Normalizing: chuẩn hóa, ý ở đây khi nói về công thức đổi biến. Qua phép biến đổi, bạn có một hàm mật độ được chuẩn hóa.
- Flows: luồng, ở đây đại ý nói về cách dùng chuổi các phép biến đổi khả nghịch.
Giả sử như tập dữ liệu chúng ta thu thập $\mathcal{D}=\{ \mathbf{x}^{(1)}, \ldots, \mathbf{x}^{(n)} \}$ với mỗi $\mathbf{x}^{(i)}$ là một vectơ biểu diễn dữ liệu. Để mô hình hóa mô hình sinh dữ liệu $p_{\mathbf{x}}(\mathbf{x})$ có nhiều cách. Một trong những cách phổ biến, chúng ta có thể áp dụng nguyên tắc hợp lý cực đại (maximum likelihood principle - đôi lúc có tài liệu dịch là triển vọng cực đại).
Nguyên tắc hợp lý cực đại có thể hiểu đơn giản như sau: dưới góc nhìn thống kê, một cách ngây ngô, ta có thể xem những gì ta quan sát được là bởi vì nó dể xảy ra nhất.
Trong trường hợp, dữ liệu được sinh ra độc lập và cùng một phân bố (i.i.d), ta có thể xem hàm cần tối ưu hợp lý cực đại dưới dạng tích của hàm mật độ $p_{\mathbf{x}}$, thường với các bài toán xác suất ta có thể tối ưu $\log$ của hàm hợp lý, vì lúc này ta sẽ tách từ dạng tích thành tổng, hơn nữa sẽ an toàn tính toán số hơn do đôi khi giá trị hàm mật độ đôi lúc rất nhỏ gần $0$.
Gọi $\theta$ là tập tham số cần tìm, $\ell$ là log hàm hợp lý (log likelihood function):
Hợp lý cực đại tương đương với tối ưu cực tiểu của hàm âm log hợp lý (negative loglikelihood), hay ta cần tìm một ước lượng $\hat{\theta}$ sao cho:
Tuy vậy, từ lý thuyết đến thực tiễn là cả bầu trời… nan giải, đau đầu… Thì mọi việc sẽ không dể, vẫn có nhiều vấn đề về tính toán mà ta cần lưu ý:
Tính toán khả nghịch phải thuận tiện đơn giản: nếu bạn cần lấy mẫu thì cần $g$ (chỉ cần lấy mẫu $\mathbf{z}$ và biến đổi sang $\mathbf{x} = g(\mathbf{z})$ ), trong khi các phép tính liên quan đến hàm mật độ $x$ bạn cần $g^{-1}$. Để tính toán nhẹ thì việc lấy định thức ma trận Jacobian phải nhanh, đây là một trong những phép toán nặng nề nhất trong bài này, khi mà phân bố chúng ta đối mặt có số chiều khổng lồ như ảnh số.
Phải đủ linh hoạt để biểu diển được quân bố quan tâm.
4. Giới thiệu mô hình RealNVP
Không lê thê dài dòng… giống như phim truyền hình dài tập nhưng cũng đôi phần hấp dẫn và gay cấn… như câu nói bất hủ trong văn học, thoáng chốc vài năm trôi qua, chỉ trong mấy phút đọc blog, từ khi ý tưởng Normalizing Flows hình thành nay đã trải qua nhiều thăng trầm mô hình hóa… sự cách tân luôn liên tục vận động thay đổi, sóng sau xô sóng trước, ấy thế lại có vài sự cách tân đáng chú ý! Nào hãy cùng nhau điểm qua kiến trúc RealNVP!
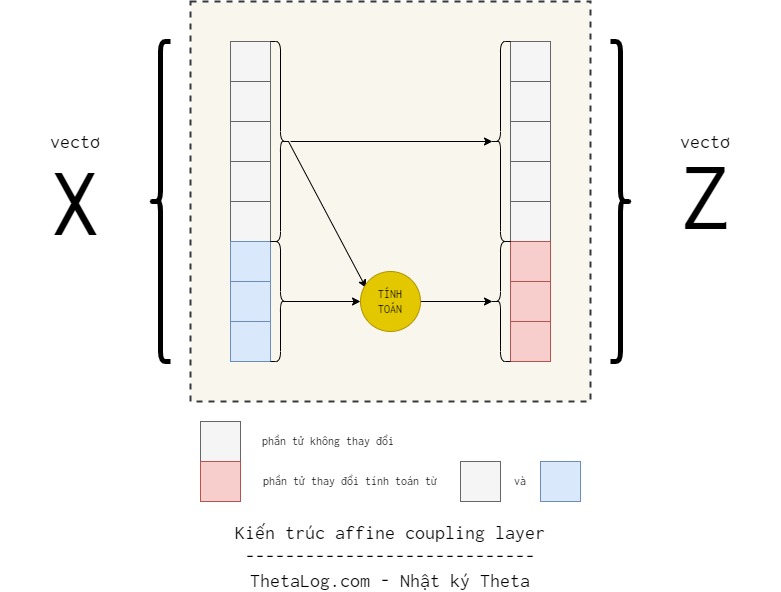
RealNVP (Real-valued Non-Volume Preserving) là một kỹ thuật trong nhóm các mô hình Normalizing Flow dùng các hàm khả nghịch lồng nhau là các lớp affine coupling layer. Sở dĩ gọi là affine coupling layer là vì phép biến đổi được tách ra làm một cặp, một phần thì giữ nguyên, một phần thì qua phép biến đổi affine.
Cụ thể $g^{-1}$ là phép biến đổi:
- $d$ phần tử đầu của vectơ giữ nguyên.
- $D-d$ phần tử còn lại từ $d+1$ đến $D$ trải qua phép biến đổi affine với tham số được học từ phần đầu tiên.
Trong đó:
- $s(.)$ và $t(.)$ lần lượt là hàm tỷ lệ (scale) và tịnh tiến (translation) ánh xạ từ $\mathbb{R}^{d} \rightarrow \mathbb{R}^{D-d}$ được mô hình hóa bởi mạng nơ-ron (neural network).
- $\odot$ là tích Hadamard. Nhân từng phần tử tương ứng của hai ma trận cùng chiều.
Khi đó phép biến đổi $g$ là:
Công thức (1) và (2) trên có thể viết gọn hơn để lúc mô hình hóa lúc lập trình trở nên đơn giản hơn bằng định nghĩa một binary mask bằng vectơ $b$ chỉ với $1$ và $0$ để xác định $d$ phần tử giữ nguyên và $D-d$ phần tử biến đổi:
Lúc này phần biến đổi ngược tương ứng:
Dể thấy $g$ và $g^{-1}$ đều không có phép tính gì phức tạp.
Hơn nữa, điều thú vị trong cách mô hình hóa của RealNVP nằm ở việc tính định thức!
Ta có ma trận Jacobian lúc này như sau:
Ma trận $J$ lúc này là ma trận tam giác dưới, tính toán định thức, từ độ phức tạp rất cao tầm $O(n^{2.373})$ theo wikipedia giờ đây nhờ việc rơi vào trường hợp đặc biệt độ phức định thức của ma trận này có thể tính bằng tích đường chéo xuống còn $O(n)$:
Dể thấy, affine coupling layer có kiến trúc thuận tiện cho việc xây dựng mô hình Normalizing Flow.
Do trong affine coupling layer, một vài chiều không thay đổi. Điều này có thể bằng cách bố trí các lớp xen kẻ nhau, sao cho các thành phần không thay đổi trong lớp này sẽ được thay đổi ở lớp kế tiếp.
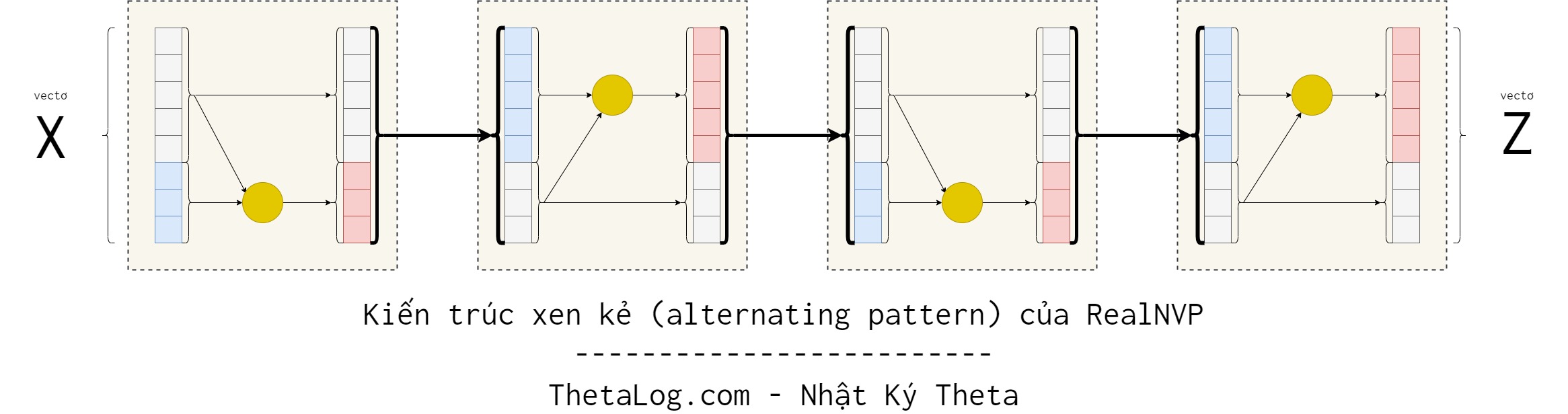
Khi đó việc tính toán định thức ma trận Jacobian $J$ từ các lớp cũng khá dể dàng, thật vậy:
Lúc này việc tính định thức bạn chỉ cần tính cho từng lớp (layer) xong rồi ghép lại thôi.
Nhìn chung kiến trúc RealNVP tương đối tốt và thuận lợi để tính toán.
Để cài đặt hoàn chỉnh RealNVP, có hai cách:
1) Tách vectơ ra thành từng phần như trên. Mình có đọc qua phần cài đặt của Tensorflow Probability theo hướng này. đọc tại dòng này
2) Cài đặt theo kiểu binary mask. Việc này giúp chúng ta tiện thử nghiệm hơn. (nếu ứng dụng cho các bài toán khác nhau, ảnh, âm thanh,… chỉ cần thay đổi binary mask).
ThetaLog quyết định chọn theo hướng thứ 2, bắt đầu vào việc nào:
import random
import tqdm
import numpy as np
from sklearn.datasets import make_moons, make_swiss_roll
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from sklearn.model_selection import train_test_split
import tensorflow as tf
import tensorflow_probability as tfp
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.layers.experimental import RandomFourierFeatures
from tensorflow.keras import regularizers, optimizers, metrics
import matplotlib.pyplot as plt
from matplotlib import cm
np_dtype = np.float32
tf_dtype = tf.float32
tfd = tfp.distributions
plt.style.use("bmh")
plt.rcParams.update({'font.size': 18})
Tái thiết lập lại thí nghiệm khi cần (mặc dù đã bật enable_op_determinism nhưng điều này còn phụ thuộc phần cứng chạy):
def alice_in_randomfield(np_seed=None, tf_seed=None):
"""Alice lạc vào xứ sở ngẫu nhiên
...điều đầu tiên cần làm là enable_op_determinism, set seed :) Cheers!
"""
if np_seed is None:
np_seed = random.randint(0, 256)
if tf_seed is None:
tf_seed = random.randint(0, 256)
np.random.seed(np_seed)
tf.keras.utils.set_random_seed(tf_seed)
# Bật chế độ tất định Tensorflow
tf.config.experimental.enable_op_determinism()
print(f"Numpy {np.__version__} set seed to {np_seed}")
print(f"Tensorflow {tf.__version__} set seed to {tf_seed}")
print(f"Tensorflow Probability {tfp.__version__}")
print("-"*28)
print("""
When the day becomes the night
And the sky becomes the sea,
When the clock strikes heavy
And there's no time for tea.
And in our darkest hour,
Before my final rhyme,
She will come back home to Wonderland
And turn back the hands of time.
""")
alice_in_randomfield(178, 149)Numpy 1.21.5 set seed to 178
Tensorflow 2.8.0 set seed to 149
Tensorflow Probability 0.16.0
----------------------------
When the day becomes the night
And the sky becomes the sea,
When the clock strikes heavy
And there's no time for tea.
And in our darkest hour,
Before my final rhyme,
She will come back home to Wonderland
And turn back the hands of time.
Tạo dữ liệu nhân tạo:
def make_synthetic_data(name_dataset, n_samples=4048, noise=0.05, dtype=np_dtype):
"""Tạo dữ liệu nhân tạo x
"""
scaler = MinMaxScaler()
if name_dataset == "Moons":
x, _ = make_moons(n_samples, noise=noise)
elif name_dataset == "EightGaussians":
sq_2 = np.sqrt(2)
c_s = 5.
centers = [(1, 0), (-1, 0), (0, 1), (0, -1),
(1. / sq_2, 1. / sq_2),
(1. / sq_2, -1. / sq_2),
(-1. / sq_2, 1. / sq_2),
(-1. / sq_2, -1. / sq_2)]
centers = [(c_s * x_1, c_s * x_2) for x_1, x_2 in centers]
x = []
for i in range(n_samples):
p = np.random.randn(2) * 0.5
idx = np.random.randint(8)
center = centers[idx]
p[0] += center[0]
p[1] += center[1]
x.append(p)
x = np.array(x)
elif name_dataset == "SwissRoll":
x = make_swiss_roll(n_samples=n_samples, noise=0.7)[0][:, [0, 2]]
elif name_dataset == "PinWheel":
std_rad = 0.3
tang_std = 0.1
n_wheel = 7
n_p_wheel = n_samples // n_wheel
r = 0.25
rads = np.linspace(0, 2 * np.pi, n_wheel, endpoint=False)
feats = np.random.randn(n_wheel * n_p_wheel, 2) * np.array([std_rad, tang_std])
feats[:, 0] += 1.
labels = np.repeat(np.arange(n_wheel), n_p_wheel)
theta = rads[labels] + r * np.exp(feats[:, 0])
rot_mat = np.stack([np.cos(theta), -np.sin(theta), np.sin(theta), np.cos(theta)])
rot_mat = np.reshape(rot_mat.T, (-1, 2, 2))
x = np.random.permutation(np.einsum("ti,tij->tj", feats, rot_mat))
x = scaler.fit_transform(x)
x = x.astype(dtype)
return x
names_dataset = ["Moons", "EightGaussians", "SwissRoll", "PinWheel"]
datasets = {name: make_synthetic_data(name) for name in names_dataset}Vẽ ra xem 4 tập dữ liệu nhân tạo trông thế nào nhé!
fig, axes = plt.subplots(1, len(names_dataset), figsize=(6 * len(names_dataset), 6),
gridspec_kw={'width_ratios': [1] * len(names_dataset)})
for i in range(len(names_dataset)):
name = names_dataset[i]
x = datasets[name]
axes[i].scatter(x[:, 0], x[:, 1], c="#007aff", s=2)
axes[i].set(title=f"{name}", xlabel="$\mathbf{x}_1$", ylabel="$\mathbf{x}_2$")
plt.show()
class RealNVPModel:
def __init__(self, D, d, n_couple_layers, z_dist=None):
"""Init Model
:param D: int - số chiều vectơ ngẫu nhiên x và z
:param d: int - số chiều giữ nguyên trong RealNVP
:param n_couple_layers: int - số layer đôi xen kẻ nhau
(số layer = số layer đôi nhân 2)
:param z_dist: tdf.Distribution - phân bố z, hoặc bất kì thư viện nào lấy log_prob.
Nếu không khai báo gì thêm sẽ lấy MultivariateNormalDiag
Lưu ý: không bất kì tham số nào z_dist là được học (cố định)
Do đó nếu như truyền vào phân bố từ tfp thì
Nhớ kiểm tra trainable_variables
Cheer!
"""
if z_dist is None:
# Khởi tạo phân bố z
z_dist = tfp.distributions.MultivariateNormalDiag(
loc=[0.0] * D, scale_diag=[1.0] * D)
self.z_distribution = z_dist
self.n_layers = n_couple_layers * 2
self.D = D
self.d = d
# binary mask cho mỗi lớp layer
self.binary_masks = np.array([
[(i + 1) % 2] * d + [(i) % 2] * (D - d)
for i in range(self.n_layers)], dtype=np_dtype)
# Hàm scale & translation tương ứng mỗi affine coupling layer
self.scale_func_list = [self.__get_scale_function()
for _ in range(self.n_layers)]
self.translation_func_list = [self.__get_translation_function()
for _ in range(self.n_layers)]
def __get_scale_function(self, l2=0.1):
"""Trả về scale function là neural network
Thoải mái viết lại hàm này! Khi thấy cần tăng, giảm độ phức tạp.
"""
assert self.D == 2, "Viết lại hàm này nhé :D Tăng phức tạp lên tí nếu cần!"
s_func = Sequential([Input(shape=self.D),
Dense(256, activation="relu",
kernel_regularizer=regularizers.l2(l2)),
Dense(256, activation="relu",
kernel_regularizer=regularizers.l2(l2)),
Dense(128, activation="tanh",
kernel_regularizer=regularizers.l2(l2)),
Dense(self.D, activation="tanh",
kernel_regularizer=regularizers.l2(l2))])
return s_func
def __get_translation_function(self, l2=0.1):
"""Trả về translation function là neural network
Thoải mái viết lại hàm này! Khi thấy cần tăng, giảm độ phức tạp.
"""
assert self.D == 2, "Viết lại hàm này nhé :D Tăng phức tạp lên tí nếu cần!"
t_func = Sequential([Input(shape=self.D),
Dense(256, activation="relu",
kernel_regularizer=regularizers.l2(l2)),
Dense(256, activation="relu",
kernel_regularizer=regularizers.l2(l2)),
Dense(128, activation="tanh",
kernel_regularizer=regularizers.l2(l2)),
Dense(self.D, activation="linear",
kernel_regularizer=regularizers.l2(l2))])
return t_func
def pdf_x(self, x):
"""Hàm mật độ xác suất p.d.f probability density function của x
"""
z, log_det = self.map_from_x_to_z_with_logdet(x)
pdf_z = self.z_distribution.prob(z)
pdf_x = pdf_z * tf.math.abs(tf.math.exp(log_det))
return pdf_x
def pdf_z(self, z):
"""Hàm mật độ xác suất p.d.f probability density function của z
"""
return self.z_distribution.prob(z)
def map_from_x_to_z_with_logdet(self, x):
"""Biến đổi x -> z qua z=g^-1(x)
:return z:
:return log_det_inv:
"""
log_det_inv = 0
z_k = x
# Biến đổi qua k layer
for k in reversed(range(self.n_layers)):
b = self.binary_masks[k]
b_x = b * z_k
s = self.scale_func_list[k]
t = self.translation_func_list[k]
z_k = b_x + (1 - b) * (z_k * tf.math.exp(s(b_x)) + t(b_x))
log_det_inv = log_det_inv + tf.reduce_sum((1 - b) * s(b_x), axis=1)
return z_k, log_det_inv
def map_from_x_to_z(self, x):
"""Biến đổi x -> z qua z=g^-1(x)
:return z:
"""
z, _ = self.map_from_x_to_z_with_logdet(x)
return z
def map_from_z_to_x_with_logdet(self, z, k_layers=None):
"""Biến đổi z -> x qua x=g(z)
:return x:
:return log_det_inv:
"""
log_det_inv = 0
x_k = z
list_layers = list(range(self.n_layers))
if k_layers:
# Chủ yếu để visualize phần sau :)
list_layers = list_layers[:k_layers]
# Biến đổi qua k layer
for k in list_layers:
b = self.binary_masks[k]
b_z = b * x_k
s = self.scale_func_list[k]
t = self.translation_func_list[k]
x_k = b_z + (1 - b) * (x_k - t(b_z)) * tf.math.exp(-s(b_z))
log_det_inv = log_det_inv - tf.reduce_sum((1 - b) * s(b_z), axis=1)
return x_k, log_det_inv
def map_from_z_to_x(self, z):
"""Biến đổi z -> x qua x=g(z)
:return x:
"""
x, _ = self.map_from_z_to_x_with_logdet(z)
return x
def sampling_z(self, n_samples):
"""Lấy mẫu z
"""
return self.z_distribution.sample(n_samples).numpy()
def sampling_x(self, n_samples):
"""Lấy mẫu x
"""
z = self.sampling_z(n_samples)
x = self.map_from_z_to_x(z)
return x
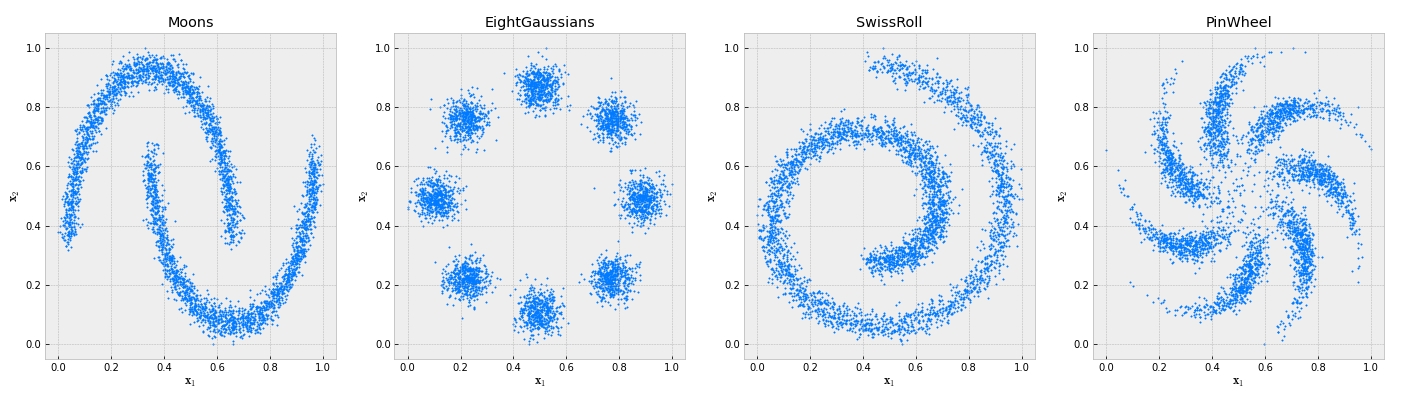
Hàm negative log likelihood:
def negative_log_likelihood(x, model):
"""Hàm âm log hợp lý (negative log likelihood)
"""
z, logdet = model.map_from_x_to_z_with_logdet(x)
log_likelihood = model.z_distribution.log_prob(z) + logdet
nll = -tf.reduce_sum(log_likelihood)
return nll
def train_real_nvp_model(dataset, test_size, batch_size, n_epochs, verbose=False):
"""Huấn luyện mô hình
:param dataset: tập dữ liệu X gồm D cột và n hàng
:param test_size: tỉ lệ validation
:param batch_size: batch_size huấn luyện
:param n_epochs: số bước tối ưu
:param verbose: có in ra dài dòng lê thê kooooo
"""
x_train, x_val = train_test_split(dataset, test_size=test_size)
n_train_samples = len(x_train)
n_validation_samples = len(x_val)
train_dataset = tf.data.Dataset.from_tensor_slices(x_train)\
.shuffle(len(x_train)).batch(batch_size)
validation_dataset = tf.data.Dataset.from_tensor_slices(x_val)\
.shuffle(len(x_val)).batch(batch_size)
# Thiết lập thuật toán tối ưu
optimizer = optimizers.Adam(learning_rate=1e-3)
# Tùy chỉnh model, bạn có thể tăng, giảm độ phức tạp n_couple_layers tùy muốn
model = RealNVPModel(D=2, d=1, n_couple_layers=3)
# Biên dịch sang callable TensorFlow graph với tf.function chạy nhanh hơn
@tf.function
def train_step(x_batch_train):
with tf.GradientTape() as tape:
loss_value = negative_log_likelihood(x_batch_train, model)
variables = tape.watched_variables()
gradients = tape.gradient(loss_value, variables)
optimizer.apply_gradients(zip(gradients, variables))
return loss_value
@tf.function
def test_step(x_batch_validation):
loss_value = negative_log_likelihood(x_batch_validation, model)
return loss_value
loss_train = []
loss_validation = []
for epoch in tqdm.tqdm(range(n_epochs)):
train_nll = 0
validation_nll = 0
for step, x_batch_train in enumerate(train_dataset):
train_nll += train_step(x_batch_train)
for x_batch_validation in validation_dataset:
validation_nll += test_step(x_batch_validation)
# tính nll cho per sample để dể quan sát so sánh
train_nll_per_sample = train_nll / n_train_samples
validation_nll_per_sample = validation_nll / n_validation_samples
loss_train.append(train_nll_per_sample)
loss_validation.append(validation_nll_per_sample)
if verbose:
tqdm.tqdm.write(
f"[{str(epoch).zfill(4)}] " +
f"train loss {'{:.6f}'.format(train_nll_per_sample)} " +
f"val loss {'{:.6f}'.format(validation_nll_per_sample)}")
return model, loss_train, loss_validation
dict_model = {}
for i in range(len(datasets)):
name = names_dataset[i]
dataset = datasets[name]
model, loss_train, loss_validation = train_real_nvp_model(
dataset, test_size=0.25, batch_size=128, n_epochs=300, verbose=False)
dict_model[name] = model, loss_train, loss_validation
Trong một xíu thời gian thưởng thức cốc trà… ngồi viết phần trực quan hóa nào…
def visualize_for_dataset(name, axes, idx_axes, model, loss_train, loss_validation):
"""Trực quan hóa dành cho ax tương ứng
"""
x_dataset = datasets[name]
axes[0, idx_axes].plot(loss_train, color="#30b0c7")
axes[0, idx_axes].plot(loss_validation, color="#a2845e")
axes[0, idx_axes].set(
title=f"Huấn luyện tập dữ liệu {name}",
xlabel="Epochs", ylabel="NLL")
axes[0, idx_axes].legend(["train", "validation"], loc="upper right")
# Biến đỗi x->z từ tập dữ liệu
z_dataset = model.map_from_x_to_z(x_dataset)
axes[1, idx_axes].scatter(x_dataset[:, 0], x_dataset[:, 1], color="#5856d6", s=2)
axes[1, idx_axes].set(
title="(1) Tập dữ liệu " + name + " $\mathbf{x}$",
xlabel="$\mathbf{x}_1$", ylabel="$\mathbf{x}_2$")
axes[2, idx_axes].scatter(z_dataset[:, 0], z_dataset[:, 1], color="#5856d6", s=2)
axes[2, idx_axes].set(
title="Biến đổi $\mathbf{z}=g^{-1}(\mathbf{x})$ từ (1)",
xlabel="$\mathbf{z}_1$", ylabel="$\mathbf{z}_2$")
axes[2, idx_axes].set_xlim([-3, 3])
axes[2, idx_axes].set_ylim([-3, 3])
# Lấy mẫu z từ phân bố nền (base distribution)
z_samples = model.sampling_z(len(x_dataset))
# Biến đổi từ z->x
x_samples = model.map_from_z_to_x(z_samples)
axes[3, idx_axes].scatter(z_samples[:, 0], z_samples[:, 1], color="#af52de", s=2)
axes[3, idx_axes].set(
title="(2) Lấy mẫu từ phân bố nền $\mathbf{z}$",
xlabel="$\mathbf{z}_1$", ylabel="$\mathbf{z}_2$")
axes[4, idx_axes].scatter(x_samples[:, 0], x_samples[:, 1], color="#af52de", s=2)
axes[4, idx_axes].set(
title="Biến đổi $\mathbf{x}=g(\mathbf{z})$ từ (2)",
xlabel="$\mathbf{x}_1$", ylabel="$\mathbf{x}_2$")
axes[4, idx_axes].set_xlim([0, 1])
axes[4, idx_axes].set_ylim([0, 1])
# Vẽ countour map
n_point = 50 # số điểm neo
min_x = 0
max_x = 1
x0_lin = np.linspace(min_x, max_x, n_point)
x1_lin = np.linspace(min_x, max_x, n_point)
x0_grid, x1_grid = np.meshgrid(x0_lin, x1_lin)
x_contour = np.hstack([x0_grid.reshape(n_point ** 2, 1),
x1_grid.reshape(n_point ** 2, 1)])
z_contour = model.pdf_x(x_contour).numpy().reshape(n_point, n_point)
axes[5, idx_axes].contourf(x0_grid, x1_grid, z_contour, cmap="OrRd", levels=100)
axes[5, idx_axes].set_xlim([0, 1])
axes[5, idx_axes].set_ylim([0, 1])
axes[5, idx_axes].set(
title="Xấp xỉ hàm mật độ $\mathbf{x}$",
xlabel="$\mathbf{x}_1$", ylabel="$\mathbf{x}_2$")
fig, axes = plt.subplots(6, len(names_dataset), figsize=(6 * len(names_dataset), 6 * 6),
gridspec_kw={'width_ratios': [1] * len(names_dataset)})
for i in range(len(datasets)):
name = names_dataset[i]
model, loss_train, loss_validation = dict_model[name]
visualize_for_dataset(name, axes, i, model, loss_train, loss_validation)
plt.show()
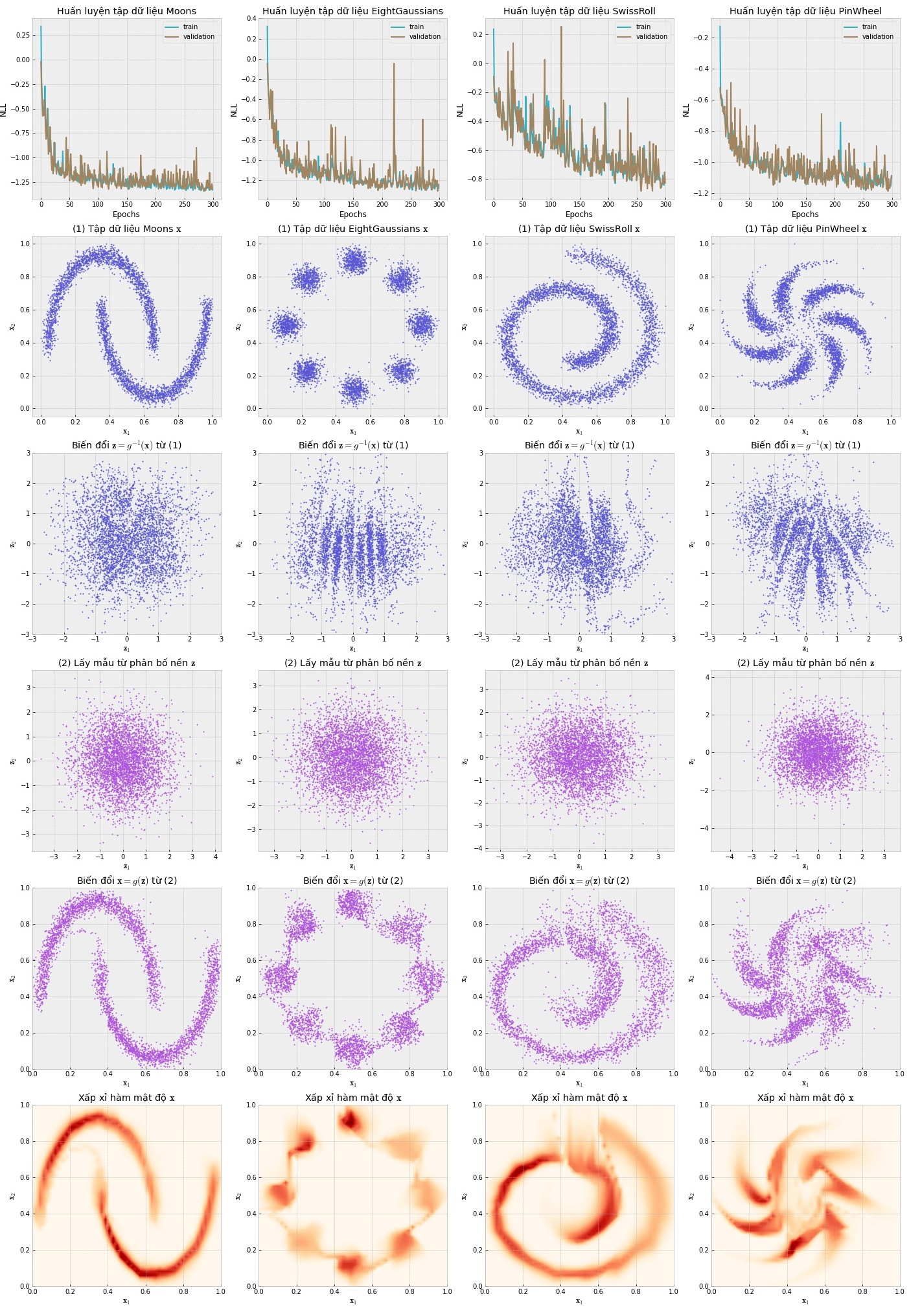
Giờ thì mô tả xem từng lớp trong mô hình mạng biến đổi các điểm dữ liệu như thế nào nhé!
plt.rcParams.update({'font.size': 30})
for name in names_dataset:
model, _, _ = dict_model[name]
cmap = cm.get_cmap('winter')
n_layers = model.n_layers
fig, axes = plt.subplots(1, n_layers+1, figsize=(6*(n_layers+1), 6*1),
gridspec_kw={'width_ratios': [1]*(n_layers+1)})
z_samples_flows = model.sampling_z(4048)
for k in range(1, 7):
x_i, _ = model.map_from_z_to_x_with_logdet(z_samples_flows, k)
x0_percentile05 = np.percentile(x_i[:,0], 2.5)
x0_percentile95 = np.percentile(x_i[:,0], 97.5)
x1_percentile05 = np.percentile(x_i[:,1], 2.5)
x1_percentile95 = np.percentile(x_i[:,1], 97.5)
axes[k].scatter(x_i[:,0], x_i[:, 1], s=5, color=cmap(k/6))
axes[k].set(title="$\mathbf{z}"+f"_{k}$")
axes[k].axes.xaxis.set_ticklabels([])
axes[k].axes.yaxis.set_ticklabels([])
axes[k].set_xlim([x0_percentile05, x0_percentile95])
axes[k].set_ylim([x1_percentile05, x1_percentile95])
axes[0].scatter(z_samples_flows[:,0], z_samples_flows[:, 1], s=2, color=cmap(0))
axes[0].set(title="$\mathbf{z}=\mathbf{z}_0$")
axes[0].axes.xaxis.set_ticklabels([])
axes[0].axes.yaxis.set_ticklabels([])
axes[n_layers].set(title="$\mathbf{z}_6=\mathbf{x}$")
axes[n_layers].set_xlim([0, 1])
axes[n_layers].set_ylim([0, 1])
plt.show()
5. Ứng dụng
Tưởng tượng là nơi mọi ứng dụng bắt đầu… Hãy tưởng tượng rằng phân bố $\mathbf{x}$ phức tạp kia nay là một đoạn âm thanh, một bức ảnh, một vần thơ, một thị trường… và hãy nhớ rằng… sự sáng tạo của bạn là then chốt của ứng dụng… vì quyền làm gì với $p_{\mathbf{x}}(\mathbf{x})$ nằm trong lòng bàn tay của bạn… xào nấu nướng ra bất kì ứng dụng nào hữu ích… tùy theo trí tưởng tượng đưa ta đi đâu.
Một số mô hình Normalizing Flows thành công có thể tham khảo:
Glow (OpenAI): dựa trên kiến trúc RealNVP (Yeahhhh, mới viết xong haha), Glow của OpenAI có nhiều ứng dụng thú vị có thể vọc vạch tại: https://openai.com/blog/glow/. Ngoài ra một số Notebook hay có thể đọc ở https://github.com/tensorchiefs/dl_book/blob/master/chapter_06/nb_ch06_05.ipynb
Parallel WaveNet: một mô hình âm thanh phát triển ý tưởng từ WaveNet và Inverse Autoregressive Flows. Xem tại: https://arxiv.org/abs/1711.10433.
Phần Notebook của RealNVP ThetaLog bạn có thể tải về ở đây: repo.
Hy vọng bạn đọc sẽ có những giây phút thú vị với Normalizing Flows!
ThetaLog - Nhật ký Theta
Tham khảo
- CS236, taught by Stefano Ermon and Aditya Grover, and have been written by Aditya Grover. Normalizing flow models. https://deepgenerativemodels.github.io/notes/flow/
- Lilian Weng. Flow-based Deep Generative Models. https://lilianweng.github.io/posts/2018-10-13-flow-models/
- Oliver Duerr. Probabilistic Deep Learning: With Python, Keras and TensorFlow Probability. https://github.com/tensorchiefs/dl_book
- Ivan Kobyzev, Simon J.D. Prince, Marcus A. Brubaker. Normalizing Flows: An Introduction and Review of Current Methods. https://arxiv.org/abs/1908.09257
- Ari Seff. What are Normalizing Flows?. https://www.youtube.com/watch?v=i7LjDvsLWCg
- Ivan Kobyzev, Simon J.D. Prince, Marcus A. Brubaker. Normalizing Flows: An Introduction and Review of Current Methods. https://arxiv.org/abs/1908.09257
- Eric Jang. Normalizing Flows Tutorial, Part 1: Distributions and Determinants. https://blog.evjang.com/2018/01/nf1.html
- Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio. Density estimation using Real NVP. https://arxiv.org/abs/1605.08803
- Affine Coupling. https://paperswithcode.com/method/affine-coupling
- Kevin Webster. Coursera. Probabilistic Deep Learning with TensorFlow 2. https://www.coursera.org/lecture/probabilistic-deep-learning-with-tensorflow2/coding-tutorial-normalising-flows-Fro8i