Locally Linear Embedding (LLE)

Đăng trên bởi Lê Quang Tiến 17 phút trôi qua :D
Nội dung bài viết

Locally Linear Embedding (LLE) là một thuật toán giảm chiều dữ liệu phi tuyến thuộc nhóm Manifold Learning. Manifold là gì nhỉ? Trong toán học tôpô, manifold được gọi là đa tạp. Đa tạp tôpô $d$ chiều là một không gian tôpô mà cục bộ của nó trông giống như một không gian euclidean $d$ chiều ở các điểm gần nhau. Nói một cách chính xác, theo ngôn ngữ tôpô thì đa tạp $d$ chiều là một không gian tôpô mà mỗi điểm có lân cận đồng phôi với tập con mở của $\mathbb{R}^{d}$.

Để hiểu rõ hơn khái niệm này, hãy nghĩ về một ví dụ khá thú vị sau đây! Vì sao người cổ đại lại nghĩ bề mặt Trái Đất “bằng phẳng” trong khi thực tế nó lại gần như là “mặt cầu”? Một lí do khá đơn giản, nhìn một cách cục bộ thì có vẻ như bề mặt Trái Đất bằng phẳng chẳng khác nào không gian euclidean $2$ chiều. Tuy nhiên, cấu trúc toàn cục lại lại là mặt cầu. Mặt cầu $3$ chiều có thể xem là một đa tạp $2$ chiều.

Những thuật toán học thuộc nhóm Manifold Learning giả định rằng dữ liệu thu thập được nằm trên một không gian với số chiều nhỏ hơn bằng với số chiều đa tạp. Hay nói cách khác các thuật toán Manifold Learning đặt ra giả thuyết đa tạp, giả định này được đưa ra bằng quan sát thực nghiệm. Lưu ý là giả định này không phải lúc nào cũng đúng, việc lựa chọn thuật toán giảm chiều dữ liệu cần am hiểu về dữ liệu mình đang xử lí.

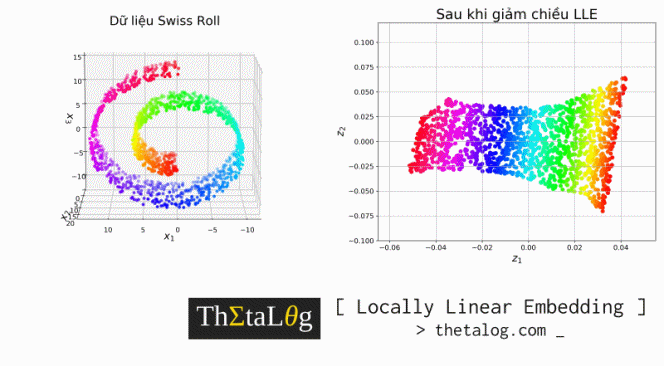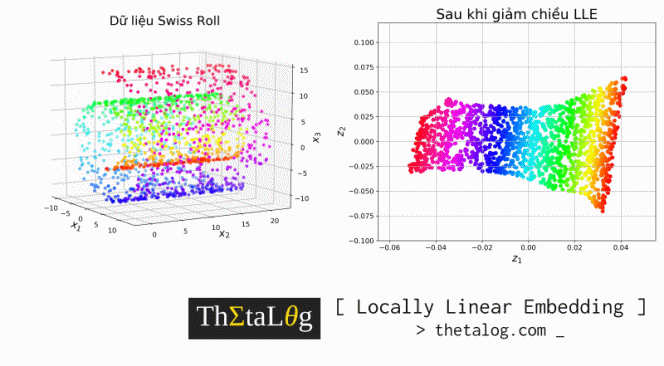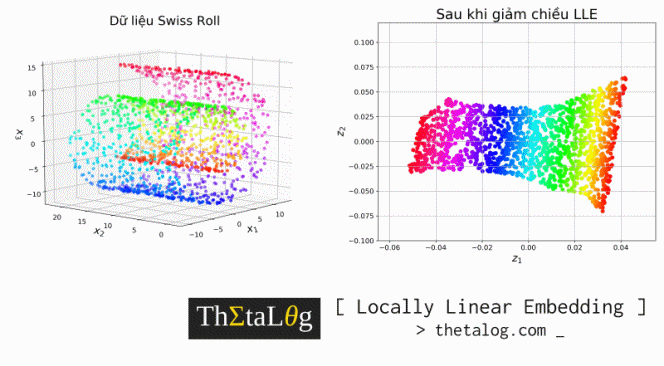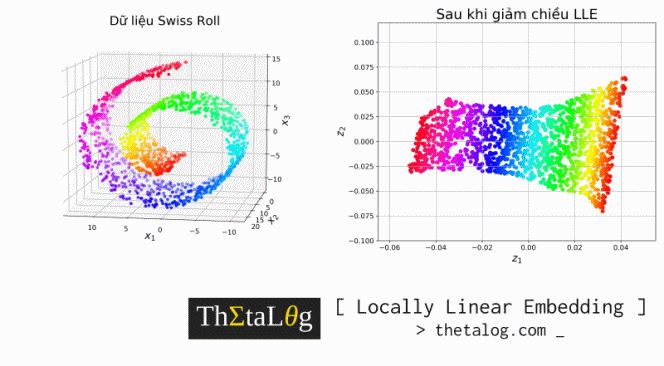
Việc chạy một thuật toán giảm chiều dữ liệu Manifold Learning tương tự như việc bạn đang có những điểm dữ liệu $3$ chiều của Trái Đất và bạn đang cố gắng vẽ lại bản đồ $2$ chiều của Trái Đất vậy!

1. Tổng quan thuật toán học Locally Linear Embedding

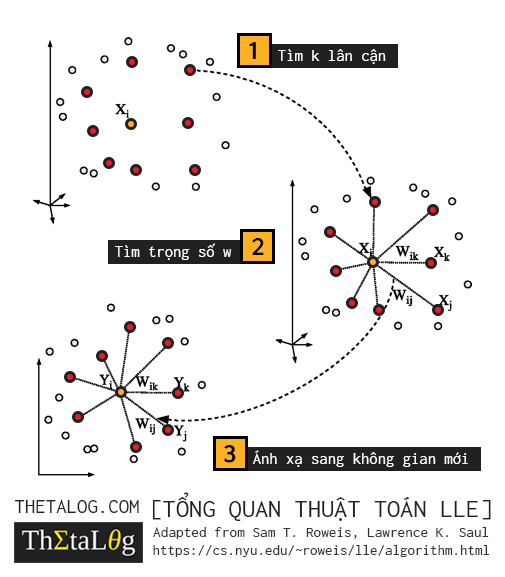
Trước khi đi vào phần diễn giải chi tiết thuật toán, chúng ta sẽ điểm qua vài điểm tổng quan của thuật toán Locally Linear Embedding.

  • Đầu vào:
    • $X$: ma trận dữ liệu $m \times D$ chiều với $m$ hàng dữ liệu, $D$ chiều thuộc tính ban đầu. Mỗi vector chuyển vị của $x^{(i)}$ ($1 \le i \le m)$ là một hàng dữ liệu của $X$.
    • $k$: số lượng lân cận láng giềng gần nhất.
    • $d$: số chiều thấp hơn muốn giảm $d$.
  • Đầu ra:
    • $Y$: ma trận giảm chiều dữ liệu $m \times d$ chiều. Mỗi vector chuyển vị của $y^{(i)}$ ($1 \le i \le m)$ là một hàng dữ liệu của $Y$.
  • Phân loại thuật toán: Manifold Learning, Học không giám sát (Unsupervised Learning), giảm chiều dữ liệu (Dimensionality Reduction).
  • Độ phức tạp thuật toán: độ phức tạp trung bình của LLE gồm 3 bước theo cách cài đặt scikit-learn là $\mathbf{O}[D\log(k) m \log(m)] + \mathbf{O}[Dmk^{3}]+\mathbf{O}[dm^{2}]$

Mã giả thuật toán có thể chia ra làm 3 bước:

  1. Tìm $k$ lân cận gần nhất với mỗi $x^{(i)}$.
  2. Tìm ma trận trọng số $W$.
  3. Tìm chiều trong không gian mới với bài toán trị riêng, vector riêng.

2. Locally Linear Embedding

Thuật toán LLE được xây dựng dựa trên ý tưởng hình học. Giả sử có $m$ vector dữ liệu huấn luyện $x^{(i)}$ (với $1 \le i \le m$), thuật toán LLE sẽ tìm $k$ lân cận gần nhất với $x^{(i)}$ và tái thiết lập $x^{(i)}$ như là một hàm tuyến tính của các điểm lân cận láng giềng.

Cụ thể hơn, thuật toán tìm trọng số $w_{i,j}$ sao cho từng bình phương khoảng cách $ \epsilon_{i} = \left\lVert x^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot x^{(j)} \right\rVert^{2} $ càng nhỏ càng tốt, hay nói cách khác tổng của các bình phương khoảng cách này nhỏ nhất:

$$ \mathcal{E}(W) = \sum_{i=1}^{m} \epsilon_{i} = \sum_{i=1}^{m} \left\lVert x^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot x^{(j)} \right\rVert^{2} $$

Với ma trận trọng số $W$ (chứa trọng số $w_{i,j}$), ràng buộc $\sum_{j}^{m} w_{i,j} = 1$ và $w_{i,j} = 0$ nếu như $x^{(j)}$ không nằm trong tập $k$ lân cận gần nhất của $x^{(i)}$.

Ý tưởng này có thể được hiểu như sau, với mỗi điểm dữ liệu $x^{(i)}$ xung quanh nó tương tự một không gian euclidean ở chiều thấp hơn, và tọa độ của nó chỉ phụ thuộc vào các điểm lân cận trong vùng cục bộ, không phụ thuộc hoàn toàn vào tất cả các điểm dữ liệu toàn cục.

Điều kiện ràng buộc $\sum_{j}^{m} w_{i,j} = 1$ lại mang ý nghĩa hình học, với điều kiện này cho phép chúng ta bất biến với phép tịnh tiến. Thật vậy nếu chúng ta tịnh tiến toàn bộ điểm dữ liệu $x^{(i)}$ theo một vector $t$ thì lúc này ta có:

$$ \left( x^{(i)} + t \right) - \sum_{j=1}^{m} w_{i,j} \cdot \left( x^{(j)} + t \right) = x^{(i)} + t - \sum_{j=1}^{m} \left( w_{i,j} \cdot x^{(j)} + w_{i,j} \cdot t \right)$$

Viết gọn lại:

$$ x^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot x^{(j)} + \left( t - t \cdot \sum_{j=1}^{m} w_{i,j} \right)$$

Điều này ngụ ý rằng khi $\sum_{j}^{m} w_{i,j} = 1$ chúng ta bất biến với phép tịnh tiến bởi vì $t - t \cdot \sum_{j=1}^{m} w_{i,j} $ triệt tiêu. Và đây là một tính chất tuyệt vời mà chúng ta muốn!

Tìm ma trận trọng số $W$
Nhiệm vụ của chúng ta là đi tìm ma trận trọng số $W$ (chứa trọng số $w_{i,j}$) sao cho: $$W = \underset{W}{\operatorname{argmin}} \mathcal{E}(W) = \underset{W}{\operatorname{argmin}} \sum_{i=1}^{m} \left\lVert x^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot x^{(j)} \right\rVert^{2} $$ Thỏa mãn điều kiện trọng số: $$\left\{ {\begin{array}{*{20}{c}} w_{i,j} = 0 \text{ nếu } x^{(j)} \text{ không nằm trong tập } k \text{ điểm lân cận gần nhất của } x^{(i)}\\\sum_{j}^{m} w_{i,j} = 1\end{array}} \right.$$

Để cực tiểu $\mathcal{E}(W)$ chúng ta sẽ đi cực tiểu từng $\epsilon_{i}$ một, hay nói cách khác:

$$ \epsilon_{i} = \left\lVert x^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot x^{(j)} \right\rVert^{2} $$

Như đã trình bày ở trên, tịnh tiến mỗi điểm dữ liệu với vector $t$ không làm thay đổi $\epsilon$, tịnh tiến mỗi điểm dữ liệu một khoảng $-x^{(i)}$ ta có:

$$ \epsilon_{i} = \left\lVert \sum_{j=1}^{m} w_{i,j} \cdot (x^{(j)} - x^{(i)} ) \right\rVert^{2} = \left\lVert \sum_{j=1}^{m} w_{i,j} \cdot z_{j} \right\rVert^{2} $$

Đặt $z_{j} = x^{(j)} - x^{(i)}$. Để tiện việc tính toán chúng ta định nghĩa một số ma trận mới như sau:

  • $\mathbf{z}_{i}$ ma trận $k \times D$ với mỗi hàng của ma trận là $k$ điểm lân cận gần nhất của $x^{(i)}$.
  • $\mathbf{w}_{i}$ ma trận $k \times 1$ chứa trọng số $w_{i,j}$, lưu ý là chúng ta chỉ quan tâm đến trọng số của $k$ điểm lân cận gần nhất vì những trọng số còn lại bằng $0$.

(lưu ý ở đây ký hiệu $\mathbf{w} \ne w$ và $\mathbf{z} \ne z$, cẩn thận tránh gây nhầm lẫn)

Khi đó $\epsilon_{i}$ có thể viết lại dưới dạng như sau:

$$\epsilon_{i} = \mathbf{w}^{\intercal}_{i} \mathbf{z}_{i} \mathbf{z}^{\intercal}_{i} \mathbf{w}_{i} $$

Lưu ý rằng $\mathbf{z}_{i} \mathbf{z}^{\intercal}_{i}$ là một ma trận Gram (Gramian matrix), chúng ta có thể ký hiệu $\mathbf{G}_{i} = \mathbf{z}_{i} \mathbf{z}^{\intercal}_{i}$, khi đó

$$\epsilon_{i} = \mathbf{w}^{\intercal}_{i} \mathbf{G}_{i} \mathbf{w}_{i} $$

Để tối tiểu $\epsilon_{i}$ chịu điều kiện giới hạn $\sum_{j}^{m} w_{i,j} = 1$ chúng ta có thể sử dụng phương pháp nhân tử Lagrange. Để trình bày dưới dạng ma trận, chúng ta ký hiệu ma trận $q \times 1$ với tất cả phần tử đều là $1$ bằng ký hiệu $\mathbf{1}$. Khi đó chúng ta có thể viết lại ràng buộc Lagrange dưới dạng $\mathbf{1}^{\intercal} \mathbf{w}_{i} = 1$ hay: $$\mathbf{1}^{\intercal} \mathbf{w}_{i} - 1 = 0$$

Khi đó Lagrangian của bài toán này là:

$$\mathcal{L}\left(\mathbf{w}, \lambda \right) = \mathbf{w}^{\intercal}_{i} \mathbf{G}_{i} \mathbf{w}_{i} - \lambda (\mathbf{1}^{\intercal} \mathbf{w}_{i} - 1)$$

Lấy đạo hàm theo giải tích ma trận, lưu ý $\mathbf{G}_{i}$ là ma trận đối xứng, cực tiểu của bài này thỏa:

$$\frac{\partial \mathcal{L}}{\partial \mathbf{w}_{i}} = 2 \mathbf{G}_{i} \mathbf{w}_{i} - \lambda \mathbf{1} = 0$$

$$\frac{\partial \mathcal{L}}{\partial \lambda} = \mathbf{1}^{\intercal} \mathbf{w}_{i} - 1 = 0$$

Hay nói cách khác:

$$\mathbf{G}_{i}\mathbf{w}_{i} = \frac{\lambda}{2} \mathbf{1}$$

Nếu $\mathbf{G}_{i}$ là ma trận khả nghịch, khi đó lời giải của ma trận trọng số của $k$ điểm lân cận gần nhất $x^{(i)}$ là:

$$\mathbf{w}_{i} = \frac{\lambda}{2} \mathbf{G}_{i}^{-1} \mathbf{1}$$

Khi đó chúng ta có thể điều chỉnh $\lambda$ để kết quả cuối cùng thỏa mãn tổng các phần tử của $\mathbf{w}_{i}$ bằng $1$. (ban đầu chọn $\lambda = 1$ sau đó tính $\mathbf{w}_{i}$ tính tổng của nó và cuối lấy $\mathbf{w}_{i}$ chia cho tổng để chuẩn hóa về $1$).

Lưu ý, thông thường khi khi $k > D$ thì tập vector của $x^{(i)}$ và $k$ điểm lân cận gần nhất phụ thuộc tuyến tính, do đó lúc này sẽ có vô số lời giải giải trọng số có thể có!

Đến đây, bạn có thể cảm giác rằng lời giải bài toán tối ưu mà chúng ta đang giải là “bất ổn định”, bởi vì có vô số lời giải, việc tìm một lời giải tối ưu trong một không gian như trên không dể. Một kỹ thuật thường dùng để giải quyết những bài toán trên là bình thường hóa bài toán Tikhonov regularization, nó sẽ giúp chúng ta có lời giải ổn định hơn bằng cách thêm vào hàm mục tiêu một tổng bình phương trọng số.

Khi $k>D$ hàm mục tiêu trở thành:

$$\mathbf{w}^{\intercal}_{i} \mathbf{G}_{i} \mathbf{w}_{i} + \alpha \mathbf{w}^{\intercal}_{i}\mathbf{w}_{i}$$

Với $\alpha$ là bậc regularization, thông thường chúng ta chọn $\alpha \in \left[ 10^{-3}, 10^{-1} \right]$

Khi đó Lagrangian của bài toán này là:

$$\mathcal{L} = \mathbf{w}^{\intercal}_{i} \mathbf{G}_{i} \mathbf{w}_{i} + \alpha \mathbf{w}^{\intercal}_{i}\mathbf{w}_{i} - \lambda (\mathbf{1}^{\intercal} \mathbf{w}_{i} - 1)$$

Tương tự, lời giải ma trận trọng số $\mathbf{w}_{i}$ là:

$$\mathbf{w}_{i} = \frac{\lambda}{2} \left( \mathbf{G}_{i} + \alpha \mathbf{I} \right)^{-1} \mathbf{1}$$

Sau khi hoàn tất việc tìm trọng số, chúng ta mong muốn một tập các điểm dữ liệu mới trong không gian mới bảo toàn quan hệ tuyến tính cục bộ của các điểm dữ liệu. Điều này dẫn đến ý tưởng xây dựng một hàm mục tiêu mới giúp chúng ta hoàn thành mục tiêu này.

Gọi $y^{(i)}$ là điểm dữ liệu $d$ chiều (với $d<D$) tương ứng của $x^{(i)}$ sau khi ánh xạ sang không gian mới, $Y$ là ma trận $m \times d$ với mỗi dòng là vector dòng của $y^{(i)}$. Chúng ta mong muốn các điểm dữ liệu trong không gian mới thỏa mãn tính chất sau đây:

Giảm chiều dữ liệu nhưng vẫn bảo tồn quan hệ tuyến tính cục bộ
Tìm các điểm dữ $y^{(i)}$ của ma trận $Y$ tối tiểu hàm $\Phi(Y)$: $$ Y = \underset{Y}{\operatorname{argmin}} \Phi(Y) = \sum_{i=1}^{m} \left\lVert y^{(i)} - \sum_{j=1}^{m} w_{i,j} \cdot y^{(j)} \right\rVert^{2} $$

Liệu việc đưa ra hàm mục tiêu như trên là đủ để chúng ta có thể tìm $y^{(i)}$ hay chưa? Có vô số lời giải cho bài toán trên, vì chúng ta có thể tịnh tiến tất cả điểm $y^{(i)}$ theo một vector $\vec{t}$ bất kì và thu được một lời giải mới mà giá trị của $\Phi(Y)$ không thay đổi!

Để tránh suy biến, chúng ta đưa thêm một điều kiện đặc biệt sau đây:

$$ \frac{1}{m} \sum_{i} y^{(i)} = 0$$

Một điều kiện khác tránh suy biến, mà chúng ta mong muốn có, đó chính là ma trận hiệp phương sai của $Y$ là ma trận đơn vị:

$$ \frac{1}{m} Y^{\intercal} Y = \mathbf{I}_{d}$$

Trước khi suy nghĩ về bài toán giảm xuống $d$ chiều, trước hết chúng ta hãy cùng nhau phân tích bài toán giảm về một chiều $d=1$ và khi đó $y^{(i)}$ là một đại lượng vô hướng, sau đó chúng ta sẽ dẫn dắt lời giải khi $d=1$ đến lời giải $d>1$, hãy kiên nhẫn. Với giả định trên $Y$ là một ma trận $m \times 1$ viết $\Phi(Y)$ lại dưới dạng ma trận:

$$\Phi(Y) = Y^{\intercal} (I - W)^{\intercal} (I - W) Y$$

Đặt $M = (I - W)^{\intercal} (I - W)$ khi đó $M$ là một ma trận $m \times m$. Ta có:

$$\Phi(Y) = Y^{\intercal} M Y$$

Lagrangian của bài toán này với các ràng buộc trên (lưu ý tạm thời chúng ta sẽ bỏ ra ràng buộc $ \frac{1}{m} \sum_{i} y^{(i)} = 0$ vì nghiệm bài có một số tính chất đặc biệt dẫn đến ràng buộc này không cần thiết, phần này sẽ được giải thích sau) với giả định $d=1$ thì $\mathbf{I}_{d} = 1$:

$$\mathcal{L}\left(Y, \mu \right) = Y^{\intercal} M Y - \mu \left( \frac{1}{m} Y^{\intercal} Y - 1 \right)$$

Lấy đạo hàm theo giải tích ma trận ta có:

$$\frac{\partial \mathcal{L}}{\partial Y} = 2 MY - 2 \frac{\mu}{n} Y = 0$$

Hay nói cách khác:

$$ MY = \frac{\mu}{n} Y$$

Phương trình trên, bạn có cảm giác quen thuộc không? Nó giống phương trình của trị riêng, vector riêng không?

Nghiệm $Y$ của bài toán này là một vector riêng của $M$ với trị riêng $\mu / n$ (lưu ý $Y$ hiện tại đang là vector $m \times 1$, cẩn thận nhầm lẫn).

Thông thường $M$ là ma trận $ m \times m$ sẽ có $m$ cặp trị riêng - vector riêng. Đặc biệt trong trường hợp này vì $M$ là ma trận đối xứng, nên các cặp vector riêng của hai trị riêng phân biệt trực giao nhau từng đôi một!

Chứng minh
Gọi $v_{1}$, $v_{2}$ lần lượt là hai vector riêng của hai trị riêng phân biệt $\lambda_{1}$, $\lambda_{2}$ của ma trận đối xứng $A$ (với số chiều $n \times n$). Chúng ta sẽ chứng minh rằng $v_{1}$, $v_{2}$ trực giao nhau, hay nói cách khác tích vô hướng của nó bằng $0$: $v_{1} \cdot v_{2} = 0$.

Thay vì chứng minh bài toán ban đầu chúng ta sẽ chứng minh $\lambda_{1} v_{1} \cdot v_{2} = 0$
Vì $v_{1}$ và $v_{2}$ là hai vector cột nên chúng ta có thể viết lại tích vô hướng dưới dạng sau:
$$ \lambda_{1} v_{1} \cdot v_{2} = (\lambda_{1} v_{1})^{\intercal} v_{2}$$ Từ khi $v_{1}$, $v_{2}$ là vector riêng nó thỏa: $A v_{1} = \lambda_{1} v_{1}$ và $A v_{2} = \lambda_{2} v_{2}$ khi đó:$$\begin{array}{*{20}{l}} \lambda_{1} v_{1} \cdot v_{2} & = (\lambda_{1} v_{1})^{\intercal} v_{2} \\ & = (A v_{1})^{\intercal} v_{2} = v_{1}^{\intercal} A^{\intercal} v_{2} \\ &= v_{1}^{\intercal} (A v_{2}) & \text{(vì } A^{\intercal} = A \text{)} \\ & = v_{1}^{\intercal} \lambda_{2} v_{2} = \lambda_{2} v_{1}^{\intercal} v_{2} \\ & = \lambda_{2} v_{1} \cdot v_{2}\end{array}$$
Vì $\lambda_{1}$ và $\lambda_{2}$ là hai trị riêng phân biệt nên $\lambda_{1}-\lambda_{2} \ne 0$, mà ta lại có: $$\left( \lambda_{1}-\lambda_{2} \right) v_{1} \cdot v_{2} = 0$$Hay nói cách khác: $v_{1} \cdot v_{2} = 0$ (điều cần phải chứng minh).

Một cặp trị riêng, vector riêng đặc biệt trong bài toán này là trị riêng $0$ và vector riêng $\mathbf{1}$. Thật vậy:

$$(\mathbf{I} - W) \mathbf{1} = \vec{0}$$ $$\Rightarrow (\mathbf{I} - W)^{\intercal} (\mathbf{I} - W) \mathbf{1} = \vec{0}$$

Hay nói cách khác $M \mathbf{1} = 0 \mathbf{1}$. Từ khi vector riêng này luôn là một hằng không thay đổi, nó thực sự không hữu ích trong việc mang lại bất kì thông tin gì trong bài toán giảm chiều dữ liệu mà chúng ta mong muốn.

Với bài toán $d>1$ việc chúng ta cần thiết là tìm $d+1$ vector riêng với trị riêng nhỏ nhất (bởi vì trị riêng nhỏ nhất là $0$ và đồng thời bài toán mà chúng ta đang giải là tối tiểu hàm mục tiêu) sau đó lấy $d$ vector riêng còn lại làm chiều mới cho dữ liệu.

Với điều kiện tránh suy biến ban đầu mà chúng ta thảo luận, trong trường hợp này điều kiện ma trận hiệp phương sai bằng $\mathbf{I}_{d}$ tự động thỏa mãn. Bởi vì các vector riêng của các trị riêng phân biệt trong bài toán này trực giao từng đôi một với nhau.

Điều gì đã xảy ra với điều kiện tránh suy biến trung bình $ \frac{1}{m} \sum_{i} y^{(i)} = 0$? Tại sao chúng ta không ràng buộc vào bài toán trên?

Nếu để ý kỹ thì dạng trung bình của các vector $y^{(i)}$ phải là vector $\vec{0}$ chúng ta có thể viết lại với dạng $\frac{1}{m} Y^{\intercal} \mathbf{1}$. Điều đặc biệt thú vị của bài toán này là mỗi cột của $Y$ giờ đây là một vector riêng của $M$, hơn nữa lại tồn tại một vector riêng đặc biệt là $\mathbf{1}$ phần chứng minh phía trên và một cặp vector riêng của hai trị riêng phân biệt thì trực giao nhau. Nó dẫn đến điều kiện ban đầu chúng ta đặt ra tự động thỏa mãn!

3. Cài đặt thuật toán

Thuật toán LLE, nếu bạn không muốn tự cài đặt lại có thể sử dụng các gói thư viện hổ trợ:

  • Python: Scikit-Learn hổ trợ LLE ở trong Manifold Learning.
  • R-lang: RDRToolbox là một thư viện cài đặt sẳn thuật toán LLE.

Phần dưới đây là một cài đặt đơn giản mà mình tự lập trình, bạn có thể tham khảo:

Trước hết là nạp các thư viện cần thiết:

#Nạp các thư viện
import numpy as np
import scipy
import sklearn
import matplotlib

# in ra phiên bản các thư viện đang sử dụng
print('Numpy: %r' % np.__version__)
print('Scipy: %r' % scipy.__version__)
print('Sklearn: %r' % sklearn.__version__)
print('Matplotlib: %r' %matplotlib.__version__)

from sklearn import neighbors, datasets
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

Phiên bản các thư viện mà ThetaLog đang sử dụng trong bài này:

  • Numpy: ‘1.14.3’
  • Scipy: ‘1.1.0’
  • Sklearn: ‘0.19.1’
  • Matplotlib: ‘2.2.2’

Thuật toán LLE chúng ta có thể cài đặt như sau:

#   _______________________________________________________________________
#  |[] ThetaLogShell                                                 |X]|!"|
#  |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
#  | > ThetaLog.com                                                      | |
#  | > ENV: Python 3.6.5 Anaconda                                        | |
#  | > Locally Linear Embedding                                          | |
#  |_____________________________________________________________________|/

def locally_linear_embedding(X, d, k, alpha=0.1):
    """
    Thuật toán Local Linear Embeddings

    :param X: numpy.ndarray - ma trận dữ liệu đầu vào m hàng, D thuộc tính
    :param d: int - số chiều giảm xuống
    :param k: int - k điểm lân cận gần nhất
    :param alpha: float - hệ số Tikhonov regularization

    :return Y: numpy.ndarray - ma trận m hàng, d thuộc tính được giảm chiều
    """
    # Bước 1: tìm k lân cận gần nhất
    # Dùng từ thư viện sklearn: from sklearn import neighbors
    x_neighbors = neighbors.kneighbors_graph(X, n_neighbors=k)

    m = len(X)
    # Bước 2: Tính trọng số
    W = np.zeros(shape=(m, m))

    for i, nbor_row in enumerate(x_neighbors):
        # lấy tập index k láng giềng của i
        k_indices = nbor_row.indices
        # Tính ma trận Z
        Z_i = X[k_indices] - X[i]

        # Tính ma trận G
        G_i = Z_i @ Z_i.T

        w_i = scipy.linalg.pinv(G_i + alpha * np.eye(k)) @ np.ones(k)
        W[i, k_indices] = w_i / w_i.sum()

    # Tính ma trận M
    M = (np.eye(m) - W).T @ (np.eye(m) - W)
    M = M.T

    # Tìm trị riêng vector riêng dùng thư viện 
    _, vectors = scipy.linalg.eigh(M, eigvals=(0, d))

    # Trả về kết quả, bỏ đi cột đầu tiên của ma trận
    return vectors[:, 1:]

Tạo dữ liệu mẫu và chạy thử thuật toán:

# Tạo tập dữ liệu Swiss Roll
m = 2500
X, color = datasets.samples_generator.make_swiss_roll(n_samples = m, noise = 0)

Chạy thuật toán Locally Linear Embedding:

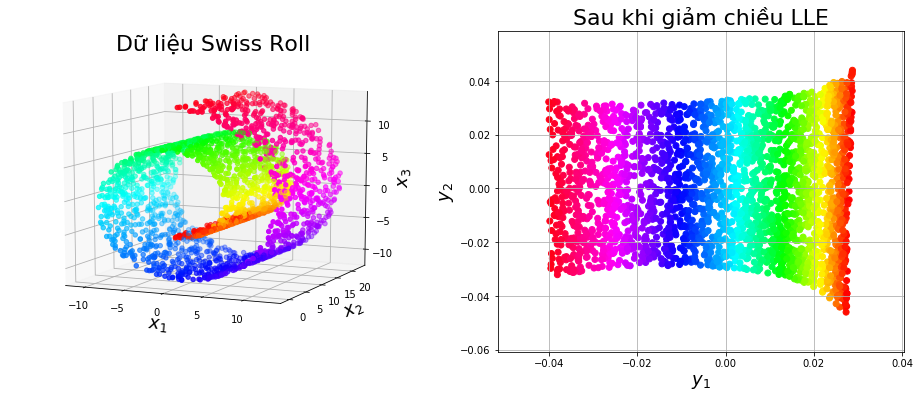
Y = locally_linear_embedding(X=X, d=2, k=20, alpha=0.1)

Visualize dữ liệu ban đầu (bên trái) và dữ liệu sau khi giảm chiều (bên phải):

fig = plt.figure(figsize=(16,13))

# Subplot đầu tiên
ax = fig.add_subplot(2, 2, 1, projection='3d')
axes = [-12, 14, -2, 24, -12, 14]
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.hsv)
ax.view_init(10, -66)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
ax.set_title("Dữ liệu Swiss Roll", fontsize=22)

# Subplot thứ hai
ax = fig.add_subplot(2, 2, 2)
ax.scatter(Y[:, 0], Y[:, 1], c = color, cmap = plt.cm.hsv)
ax.set_xlabel("$y_1$", fontsize=18)
ax.set_ylabel("$y_2$", fontsize=18)
ax.grid(True)
ax.set_title("Sau khi giảm chiều LLE", fontsize=22)

plt.show()

Kết quả thu được:

4. Một số công trình

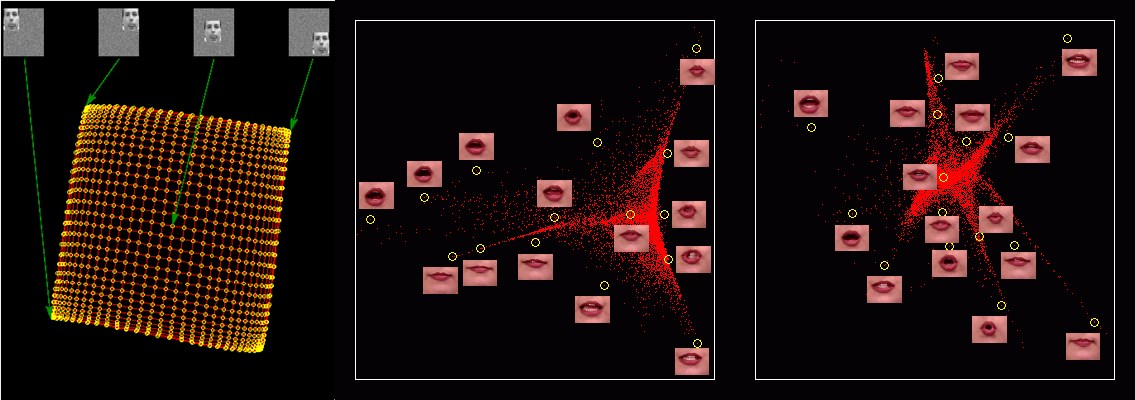
Một số công trình nghiên cứu về ứng dụng của Locally Linear Embedding các bạn có thể tìm thấy ở: https://cs.nyu.edu/~roweis/lle/gallery.html.

Kết quả trên là những công trình nghiên cứu về giảm chiều dữ liệu để visualize sang $2$ chiều. Như chúng ta thấy các điểm dữ liệu trong không gian mới bảo tồn tính chất phụ thuộc tuyến tính cục bộ (giữa hai khung hình khi di chuyển môi là không mấy khác biệt, và mỗi điểm dữ liệu có thể biểu diễn lại phụ thuộc tuyến tính vào các điểm dữ liệu lân cận, tuy nhiên càng xa lại càng khác biệt).

5. Tổng kết

Thuật toán Locally Linear Embedding là một thuật toán Manifold Learning, nó đặt ra giả thuyết dữ liệu tồn tại một đa tạp $d$ chiều, thuật toán cố gắng ánh xạ dữ liệu ban đầu sang không gian mới mà vẫn bảo toàn tính chất phụ thuộc tuyến tính cục bộ của dữ liệu. Điểm yếu lớn nhất của thuật toán này là không phù hợp với các bài toán dữ liệu cực lớn khi mà độ phức tạp không hề nhỏ.

Tham khảo

  1. Ryan Tibshirani. Nonlinear Dimensionality Reduction I: Local Linear Embedding 36-350, Data Mining. 5 October 2009. https://www.stat.cmu.edu/~cshalizi/350/lectures/14/lecture-14.pdf

  2. Rowland, Todd. “Manifold.” From MathWorld–A Wolfram Web Resource, created by Eric W. Weisstein. http://mathworld.wolfram.com/Manifold.html

  3. Roweis, S. & Saul, L. “Nonlinear dimensionality reduction by locally linear embedding”. Science 290:2323 (2000)

  4. Wikipedia contributors. “Manifold.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 10 Jul. 2018. Web. 28 Aug. 2018.

  5. Wikipedia contributors. “Matrix calculus.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 6 Jul. 2018. Web. 30 Aug. 2018.