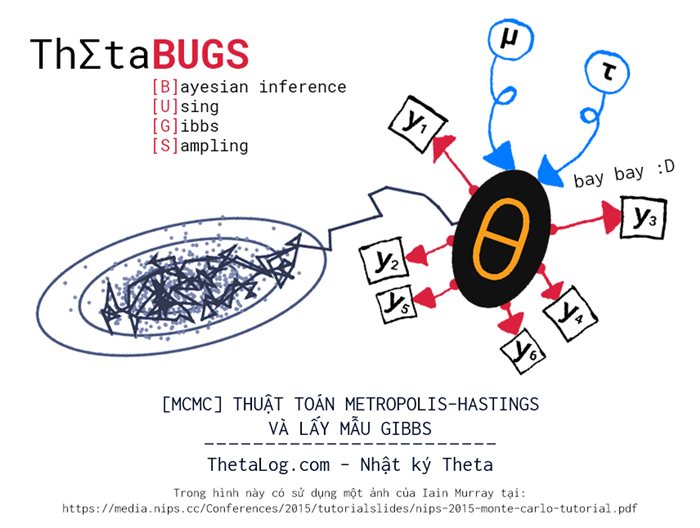
MCMC Thuật toán Metropolis–Hastings và lấy mẫu Gibbs
Nội dung bài viết
Markov Chain Monte Carlo (MCMC) là một họ gồm nhiều thuật toán thường dùng để lấy mẫu phân bố xác suất nhiều chiều dựa trên việc xây dựng xích Markov có phân bố dừng tương ứng và kỹ thuật gieo điểm ngẫu nhiên Monte Carlo. Theo một khảo sát của SIAM News (Society for Industrial and Applied Mathematics) về xếp hạng 10 thuật toán ảnh hưởng nhất thế kỷ 20, sự ra đời Metropolis–Hastings (thuật toán MCMC đầu tiên) giữ vai trò quan trọng trong kỷ nguyên tính toán.
Lịch sử phát triển các kỹ thuật Markov Chain Monte Carlo là một hành trình dài và đầy thú vị, những kỹ thuật này xuất hiện từ rất sớm, tuy nhiên người ta không nhận ra sức mạnh của nó cho mãi đến khi tầm nhìn sức mạnh tính toán của máy tính bắt đầu thay đổi đáng kể vào những năm 1990.
Thuật toán đầu tiên là Metropolis được tìm ra bởi các nhà vật lý trong khi làm việc với bom nguyên tử ở Los Alamos trong thế chiến thứ II lần đầu tiên xuất hiện trong một tập san hóa học 1953, đến mãi 1970 phần mở rộng của nó được Hasting nghiên cứu xuất hiện trong cộng đồng khoa học thống kê, nhưng phần lớn không ai quan tâm đến. Một trong những trường hợp đặc biệt của Metropolis–Hastings là Gibbs Sampling (trong cộng đồng vật lý, người ta thường biết với cái tên Glauber dynamics), thuật toán được mô tả bởi hai anh em Stuart và Donald Geman vào 1984 sau tám thập niên sau khi nhà vật lý học Josiah Willard Gibbs qua đời.
Ý tưởng cơ bản của thuật toán là gieo điểm ngẫu nhiên và dịch chuyển ngẫu nhiên dựa trên những dự định xem là hợp lí.
1. Một ý tưởng chưa hoàn tất
Một vương quốc bọ nọ gồm nhiều vùng lãnh thổ khác nhau. Mỗi vùng lãnh thổ có thể đi về hướng đông hoặc hướng tây để sang một vùng lãnh thổ mới. Nghĩa vụ của bọ chúa trong đàn là:
- Mỗi tuần phải viếng thăm một vùng lãnh thổ của vương quốc, công du mỗi vùng đất để hiểu về tình hình vương quốc.
- Đảm bảo công bằng giữa mỗi vùng lãnh thổ. Vùng nào dân số nhiều hơn thì sẽ được viếng thăm nhiều hơn , vùng nào ít hơn thì ít ưu tiên hơn.
- Lịch trình phải luôn ngẫu nhiên, không cố định… như vậy mới là một vị quốc vương thú vị, và cũng có lẽ như vậy thì mới đảm bảo được an toàn.
Liệu có một mẹo giải đơn giản nào có thể giải bài toán trên?
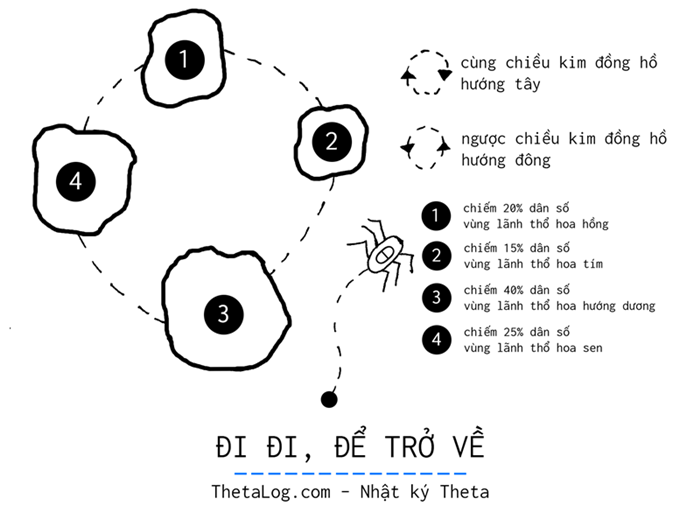
Với $20 \%$ dân số nằm ở cánh đồng hoa hồng, $15\%$ dân số ở cánh đồng hoa tím, $40\%$ dân số nằm ở cánh đồng hoa hướng hướng dương và $25\%$ ở đầm sen. Một lịch trình ngẫu nhiên nhưng cuối cùng lại xấp xĩ được phân bố mà chúng ta mong muốn, liệu có cách đơn giản nào có thể giải bài toán này?
Phân tích một chút nhé:
Tại thời điểm ban đầu, không có thông tin gì, chúng ta chọn xuất phát điểm tại một địa điểm bất kì.
Lặp đi lặp lại quá trình sau:
2.1 Tương lai phụ thuộc vào những dự định. Khả năng có thể xảy ra là bạn sẽ ở lại địa điểm hiện tại hoặc di chuyển về hướng tây hoặc hướng đông. Nhưng nếu di chuyển thì hướng đông hay hướng tây là sự lựa chọn? Chúng ta cần quy tập những địa điểm có thể đến thành một dự định duy nhất, cuối cùng xét nên di chuyển hay không để đưa ra quyết định. Trong trường hợp thực tế, có thể số địa điểm có thể đến rất lớn, bạn không đủ thời gian để so sánh chi li từng nơi.
Hãy để đồng xu đưa ra sự lựa chọn, chỉ cần xấp và ngửa ta sẽ biết tây hay đông là nơi dự định đến!2.2 Nếu như địa điểm dự định đến có tỷ lệ dân số lớn hơn hẳn so với địa điểm hiện tại, xem ra chúng ta nên đến địa điểm mới hơn. Trường hợp còn lại, khi tỷ lệ dân số nơi dự định đến (gọi là $\mathtt{p}_{\mathtt{proposed}}$) nhỏ hơn tỷ lệ dân số địa điểm hiện tại (gọi là $\mathtt{p}_{\mathtt{current}}$), chúng ta có phần lưỡng lự, chúng ta chỉ quyết định di chuyển với một xác suất $\mathtt{p}_{\mathtt{move}} = \mathtt{p}_{\mathtt{proposed}} / \mathtt{p}_{\mathtt{current}}$.
Theo bạn, lời giải trên có thực sự hoạt động hay không? Hãy chạy thử mã nguồn dưới đây để kiểm tra thử nhé!
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: Python 3.7.0 (Anaconda) | |
# | > Ý tưởng đơn giản MH Algorithm | |
# |_____________________________________________________________________|/
import random
from collections import Counter
MAX_LAND = 4
HEAD = 1
TAIL = 0
pmf = [0.2, 0.15, 0.4, 0.25]
label = ['rose', 'violet', 'sunflower', 'lotus']
def flip_a_coin():
return random.randint(0, 1)
def to_the_west(index):
if index - 1 == -1:
return MAX_LAND - 1
else:
return index - 1
def to_the_east(index):
if index + 1 == MAX_LAND:
return 0
else:
return index + 1
def heuristics_solution(n_samples = 1000):
samples = []
current_land = random.randint(0, MAX_LAND - 1)
samples.append(current_land)
for i in range(n_samples):
coin = flip_a_coin()
if coin == HEAD:
proposal_land = to_the_east(current_land)
else:
proposal_land = to_the_west(current_land)
if pmf[proposal_land] > pmf[current_land]:
samples.append(proposal_land)
current_land = proposal_land
else:
if random.uniform(0, 1) <= pmf[proposal_land] / pmf[current_land]:
samples.append(proposal_land)
current_land = proposal_land
else:
samples.append(current_land)
return samples
if __name__ == '__main__':
n_samples=100000
samples = heuristics_solution(n_samples)
counter = Counter(samples)
print('-'*10 + 'Sampling Distribution' + '-'*10)
for i in range(MAX_LAND):
print('%s: %f' %(label[i], counter[i]/n_samples))# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: R version 3.5.0 | |
# | > Ý tưởng đơn giản MH Algorithm | |
# |_____________________________________________________________________|/
# có 4 vùng đất
MAX_LAND = 4
# xác suất mỗi vùng
pmf <- c(0.2, 0.15, 0.4, 0.25)
label <- c("rose", "violet", "sunflower", "lotus")
# hàm tung một đồng xu
flip_a_coin <- function(){
return(sample(x = c("HEAD", "TAIL"), size = 1))
}
# về hướng tây
to_the_west <- function(index){
if (index - 1 == 0){
return(MAX_LAND)
}
else {
return(index - 1)
}
}
# về hướng đông
to_the_east <- function(index){
if (index + 1 > MAX_LAND){
return(1)
}
else {
return(index + 1)
}
}
# mẹo giải mà chúng ta đặt ra
heuristics_solution <- function(n_samples = 10000){
current_land <- sample(x = 1:MAX_LAND, size = 1)
samples <- c(current_land)
for (i in 1:n_samples){
coin <- flip_a_coin()
if (coin == "HEAD"){
proposal_land <- to_the_east(current_land)
}
else {
proposal_land <- to_the_west(current_land)
}
if (pmf[proposal_land] > pmf[current_land]){
samples <- c(samples, proposal_land)
current_land <- proposal_land
}
else {
if (runif(1, 0, 1) <= pmf[proposal_land] / pmf[current_land]){
samples <- c(samples, proposal_land)
current_land <- proposal_land
}
else {
samples <- c(samples, current_land)
}
}
}
return(samples)
}
n_samples = 10000
result <- heuristics_solution(n_samples)
counter <- table(result) /n_samples
names(counter) <- label
print(paste0("-----", "Sampling Distribution", "-----"))
print(counter)2. Thuật toán Metropolis–Hastings
Trường hợp phía trên là trường hợp đơn giản của Metropolis–Hastings Algorithm, đọc phần dưới đây bạn sẽ thấy rằng:
- $q(x’|x)$: chính là phân bố dự định chọn Đông hay Tây bằng tung đồng xu.
- $p(x)$: chính là phân bố dân số trong bài toán trên.
- $r=(1, \alpha)$: chính là quyết định di chuyển lập tức hay di chuyển với mức lưỡng lự.
2.1 Mã giả thuật toán Metropolis–Hastings
Gọi $p$ là phân bố cần lấy mẫu với hàm mật độ xác suất $p(x)$ (hoặc hàm khối xác suất trong trường hợp $x$ rời rạc), làm sao để lấy được mẫu từ phân bố này?
Ý tưởng cơ bản của Metropolis–Hastings là ở mỗi bước chúng ta sẽ cân nhắc đưa ra dự định từ trạng thái hiện tại $x$ đến trạng thái mới $x’$ với xác suất $q(x’ | x)$ khi biết trạng thái trước $x$, với $q$ được gọi là phân bố dự định (proposal distribution).
Dự định phụ thuộc vào chúng ta - những người xây dựng trạng thái mới trong tương lai, tương tự vậy phân bố $q(x’ | x)$ là một phân bố mà do ta chọn sẽ quyết định tính ổn định của thuật toán. Thuật toán Metropolis–Hastings là một thuật toán linh động nhờ vào đây.
Phân bố thường dùng để làm phân bố dự định là phân bố chuẩn $x’ | x \sim \mathcal{N}(x, \Sigma)$ (thường là lấy isotropic gaussian tức phân bố chuẩn có hàm mật độ với $\Sigma = \sigma^2 I_n$).
Liệu dự định này có hợp lí để chúng ta chuyển sang trạng thái mới $x’$? Nếu dự định $x’$ được chấp nhận chúng ta sẽ thêm $x’$ vào tập mẫu, ngược lại chúng ta sẽ thêm $x$ trạng thái hiện tại. Khi $q$ là một phân bố đối xứng thỏa $q(x’ |x) = q(x|x’)$, việc chấp nhận hay từ chối dự định $x’$ được dựa trên xác suất được tính bởi công thức sau:
$$\color{WildStrawberry} r = \min\left\{1, \frac{p(x’)}{p(x)}\right\}$$
Công thức trên nhìn có vẻ đơn giản nhưng ý nghĩa sâu xa của nó thú vị như sau:
Nếu như xác suất xảy ra $x’$ lớn hơn so với $x$ nghĩa là $p(x’) \ge p(x)$ chúng ta sẽ lập tức chuyển sang trạng thái mới $x’$! Vì sao vậy? Vì lúc này $\frac{p(x’)}{p(x)} \ge 1$ do đó $r = \min\left\{1, \frac{p(x’)}{p(x)}\right\} = 1$.
Nếu như xác suất xảy ra $x’$ nhỏ hơn so với $x$ chúng ta đồng ý dự định với một xác suất dựa trên một suy nghĩ rất đơn giản “$x’$ phổ biến hơn so với $x$ bao nhiêu vậy?”, câu trả lời nằm ở phép chia đơn giản $\frac{p(x’)}{p(x)}$
| Ghi chú |
|---|
| Nếu bạn am hiểu lý thuyết xác suất thống kê, có lẽ bạn sẽ phát hiện ra có một thứ gì đó chưa nhất quán lắm giữa công thức phía trên và ý tưởng ban đầu! Thật vậy ý tưởng ban đầu của chúng ta xem liệu tỉ lệ cơ hội xuất hiện giữa $x'$ và $x$ như thế nào bằng cách chia tỉ lệ xác suất xuất hiện giữa chúng. Tuy nhiên điều này chỉ đúng với những biến ngẫu nhiên rời rạc, xác suất xảy ra với bất kỳ điểm dữ liệu trên phân bố liên tục luôn luôn bằng $0$ (mặc dù không có nghĩa là nó không thể xảy ra). Nhắc lại, với phân bố liên tục chúng ta tính xác suất trong vùng từ $a$ đến $b$ của hàm mật độ xác suất $p(x)$: $$\mathtt{probability} = \int_{a}^{b} p(x) dx$$ May mắn thay, giải tích toán học có thể "cứu nguy" cho pha này, thật vậy khi epsilon $\epsilon$ thật nhỏ ta có:$$p(a - \epsilon \le \mathbf{x} \le a + \epsilon) = \int_{a-\epsilon}^{a+\epsilon} p(x) dx \approx 2 \epsilon \cdot p(a)$$Vì vậy lúc này ta có: $$\mathtt{p}_{\mathtt{move}} = \frac{\mathtt{p}_{\mathtt{proposed}}}{\mathtt{p}_{\mathtt{current}}} \approx \frac{p(x')}{p(x)}$$ |
Nếu như phân bố dự định không phải là một phân bố đối xứng $q(x’ |x) = q(x|x’)$, chúng ta cần thực hiện Hastings correction (một số tài liệu gọi bước này là nhân với correction factor) bằng cách:
$$\color{WildStrawberry} r = \min\left\{1, \alpha \right\}$$
$$\color{WildStrawberry} \alpha = \frac{p(x’)/ q(x’ | x) }{p(x) / q(x | x’)} = \frac{p(x’) q(x | x’) }{p(x) q(x’ | x)}$$
Phép chuẩn hóa đơn giản này để đảm bảo “công bằng” giữa việc dịch chuyển từ trạng thái $x$ sang $x’$ hay từ $x’$ sang $x$, tránh việc thiên vị cho một số trạng thái dù phân bố dự định có sao đi chăng nữa.
Một điểm thú vị của thuật toán này là cho phép bạn có thể lấy mẫu ngay cả biến ngẫu nhiên $x$ ngay khi phân bố chưa được chuẩn hóa, chỉ cần phân bố đó tỷ lệ với phân bố gốc (nếu $x$ rời rạc thì hàm khối xác suất phải thỏa $\sum_{i} p(x) = 1$, nếu $x$ liên tục thì hàm mật độ xác suất phải thỏa $\int_{-\infty}^{+\infty} p(x) dx = 1$), gọi $w(x)$ là phân bố chưa được chuẩn hóa và $Z$ là hệ số chuẩn hóa $p(x) = \frac{1}{Z} w(x)$ lúc này ta có:
$$\alpha = \frac{p(x’)q(x|x’)}{p(x)q(x’|x)} = \frac{(w(x’)/Z)q(x|x’)}{(w(x)/Z)q(x’|x)} = \frac{w(x’)q(x|x’)}{w(x)q(x’|x)}$$
Do đó bạn hoàn toàn có thể dùng $w(x)$ để thực hiện lấy mẫu, vì thế ngoài việc lấy mẫu từ phân bố xác suất, đôi lúc thuật toán Metropolis–Hastings có thể phục vụ cho việc tính toán số (đôi lúc gọi là giải tích số - numerical analysis) để tính tích phân của một số hàm phức tạp phục vụ vật lí.
Mã giả thuật toán như sau:
Khởi tạo mẫu $x^0$
Tập mẫu $s = \{ x^0 \}$
For $i$ trong khoảng ($0$ đến $n - 1$) do:
Trạng thái hiện tại $x = x ^i$
Lấy mẫu $x' \sim q(x' | x)$
Tính $\alpha = \frac{p(x') q(x | x') }{p(x) q(x' | x)}$, trường hợp $q$ là một phân bố thỏa $q(x' | x) = q(x| x')$ tối ưu tính toán $\alpha = \frac{p(x')}{p(x)}$
Tính xác suất chấp nhận $r = \min \{ 1, \alpha \}$
Lấy mẫu phân bố đều trong đoạn $[0, 1]$ hay $u \sim \text{U}(0,1)$
Tính mẫu mới $x^{i+1} = \left\{ {\begin{array}{*{20}{c}}{x'}&{\text{nếu } u < r}\\x&{\text{nếu } u \ge r}\end{array}} \right.$
Thêm $x^{i+1}$ vào tập mẫu $s$
RETURN $s = \{ x^0, x^1,... x^{n-1} \}$
2.2 Vì sao Metropolis–Hastings hoạt động?
Phần chứng minh này là một chứng minh không chặt, sẽ chứng minh cho phân bố rời rạc, trường hợp liên tục bạn đọc tự tìm hiểu.
Phần chứng minh tính đúng đắn của thuật toán Metropolis–Hastings có thể chia ra làm $2$ ý chính:
- Thuật toán Metropolis–Hastings khi chạy tạo thành một xích Markov. Xích Markov này có phân bố dừng (stationary distribution) vì nó bất khả quy (irreducible), phi chu kỳ (aperiodic).
- Phân bố dừng của xích Markov nêu trên chính là phân bố đầu vào.
Thuật toán Metropolis–Hastings chạy tạo thành một một xích Markov, với ma trận chuyển đổi trạng thái được cho như sau:
$$ p(x’|x) = \left\{ { \begin{array}{*{20}{c}}{q(x’|x)r(x’, x)}&{\text{nếu } x’ \neq x}\\ q(x|x) + \Sigma_{x’ \neq x} q(x’|x)(1-r(x’, x)) &{\text{trường hợp còn lại}}\end{array} } \right. $$
Với $r(x’, x) = \min \left\{ 1, \frac{p(x’) q(x | x’) }{p(x) q(x’ | x)} \right\}$ là xác suất chấp nhận sau khi chọn.
Làm một phép phân tích để hiểu ý trên nhé:
Nếu dịch chuyển từ trạng thái $x$ sang $x’$, đầu tiên bạn cần phải đưa ra một dự định mới từ phân bố $q(x’|x)$, khi có $x’$ việc chấp nhận hay không lại phụ thuộc vào hệ số $r(x’, x)$. Theo quy tắc nhân chúng ta có xác suất như trên.
Nếu lấy mẫu từ $q(x’|x)$ cho ra kết quả là $x$ thì do $r(x,x) = 1$ nên do đó $x$ sẽ được thêm vào tập mẫu, đây là trường hợp đầu tiên. Trường hợp thứ hai, khi $x’$ được đưa ra nhưng bị từ chối bởi $r(x’, x)$, theo quy tắc nhân chúng ta có xác suất $q(x’|x)(1-r(x’,x))$. Theo quy tắc cộng và quy tắc nhân chúng ta có xác suất ở dòng thứ hai.
Nếu như ma trận chuyển đổi trạng thái của xích Markov bất khả quy và phi chu kỳ chúng ta chỉ cần chứng minh điều cuối cùng là $p^{*}(x)$ là phân bố dừng của xích này.
Nếu $p^{*}$ là phân bố dừng, nó sẽ thỏa phương trình detailed balance, chúng ta sẽ chứng minh phương trình sau đây đúng:
$$\color{WildStrawberry} p^{*}(x) p(x’|x) = p^{*}(x’)p(x|x’)$$
Phương trình này ngụ ý rằng xét $2$ trạng thái bất kì, xác suất đến được tới một trạng thái bất kì và dịch chuyển sang trạng thái còn lại là như nhau.
Không mất tính tổng quát, giả định rằng $p^{*}(x)q(x’|x) > p^{*}(x’)q(x|x’)$
Do đó, ta có $\alpha(x’, x) = \frac{p^{*}(x’) q(x | x’) }{p(x)^{*} q(x’ | x)} < 1$ và lúc này $r(x’, x) = \alpha(x’, x)$, $r(x, x’) = 1$.
Chúng ta sẽ cố gắng đi tính vế trái và vế phải của phương trình detailed balance!
Ta có:
$$p(x’|x) = q(x’|x)r(x’|x) = \frac{p^{*}(x’)}{p^{*}(x)}q(x|x’)$$
Do đó vế trái của phương trình:
$$\color{WildStrawberry} p^{*}(x) p(x’|x) \color{#37474f} = p^{*}(x) \frac{p^{*}(x’)}{p^{*}(x)}q(x|x’) = p^{*}(x’)q(x|x’) \tag{1}$$
Ta có:
$$p(x|x’) = q(x|x’)r(x|x’) = q(x|x’)$$
Do đó vế phải của phương trình:
$$\color{WildStrawberry} p^{*}(x’) p(x|x’) \color{#37474f} = p^{*}(x’)’ q(x|x’) \tag{2}$$
Từ $(1)$ và $(2)$ suy ra $\color{Blue} p^{*}(x) p(x’|x) = p^{*}(x’)p(x|x’)$.
Do đó nếu chúng ta đảm bảo được xích Markov được tạo ra bất khả quy (irreducible), phi chu kỳ (aperiodic) thì mọi việc xem như hoàn tất. Điều này dựa trên cách mà chúng ta lựa chọn phân bố dự định $q(x)$ và phụ thuộc hàm phân bố xác suất mục tiêu $p(x)$.
2.3 Nên chọn phân bố dự định như thế nào?
Một phân bố dự định tốt (proposal distribution) là một phân bố:
- Dể tính toán $r$.
- Tránh việc từ chối $x’$ quá thường xuyên (hội tụ chậm, mất nhiều thời gian để đứng ở một trạng thái).
- Với mọi $x$, đơn giản để lấy mẫu từ $p(x’|x)$.
3. Gibbs Sampling
Nếu như bạn bâng khuâng không biết liệu nên chọn phân bố dự định như thế nào là hợp lí và hiệu quả… có lẽ Gibbs sampling là một lựa chọn hay ho mà chúng ta có thể xem qua…
3.1 Mã giả thuật toán Gibbs Sampling
Giả sử vectơ ngẫu nhiên $x = (x_{1},… x_{d})$ có phân bố $p(x)$ là một hàm mật độ p.d.f hoặc một hàm khối xác suất p.m.f khó lấy mẫu trực tiếp.
Lưu ý rằng thuật toán Metropolis-Hasting xem $p(x)$ như một “hộp đen”, chúng ta không màn gì về cấu trúc của phân bố $p(x)$ cả, tương tự việc chọn phân bố dự định $q(x)$ thường không dựa trên cấu trúc của $p(x)$. Gibbs Sampling là một thuật toán dùng phân bố dự định dựa trên cấu trúc phân bố ban đầu $p(x)$!
Ý tưởng của Gibbs Sampling như sau:
- Tại thời điểm ban đầu $i=0$ chúng ta có vectơ $x^0 = (x^0_1,…, x^0_d)$.
Lặp đi lặp lại $n-1$ lần bước 2. - Lấy mẫu $i+1$ hay $x^{i+1}$
2.1 Xét trạng thái hiện tại $x = x^i = (x^i_1,…,x^i_d)$
2.2 Lấy mẫu $d$ chiều:
Lấy mẫu $x^{i+1}_1 \sim p(x_1 | \color{blue} x^i_2, x^i_3…,x^i_s \color{#37474f})$.
Cập nhật trạng thái hiện tại: $x = (\color{WildStrawberry} x^{i+1}_1 \color{#37474f} , x^i_2…, x^{i}_d)$
Lấy mẫu $x^{i+1}_2 \sim p(x_2 | \color{blue} x^{i+1}_1, x^i_3,…,x^i_s \color{#37474f} )$.
Cập nhật trạng thái hiện tại: $x = (\color{WildStrawberry} x^{i+1}_1, x^{i+1}_2 \color{#37474f}, x^i_3…, x^{i}_d)$
…lặp đến khi lấy xong $d$ chiều…
Mã giả thuật toán có thể trình bài như sau:
Khởi tạo mẫu $x^0$
Tập mẫu $s = \{ x^0 \}$
For $i$ trong khoảng ($0$ đến $n - 2$) do:
Trạng thái hiện tại $x = x^i = (x^i_1,...,x^i_d)$
For $j$ trong đoạn $[1,d]$ do:
Lấy mẫu $x^{i+1}_j \sim p(x_j| \mathbf{x}_{-j})$ với $\mathbf{x}_{-j}$ là tập tất cả các biến của $x$ hiện tại ngoại trừ $x_j$
Cập nhật $x^{i+1}_j$ cho $x$ hay gán $x_j \leftarrow x^{i+1}_j$
Ta có $x^{i+1} = (x^{i+1}_1,...,x^{i+1}_d)$
Thêm $x^{i+1}$ vào tập mẫu $s$
RETURN $s = \{ x^0, x^1,... x^{n-1} \}$
(lưu ý: trong một số tài liệu Gibbs Sampling được viết thay vì $j$ được xét tuần tự trong đoạn $[1,d]$ thì được lấy ngẫu nhiên từ phân bố đều trong đoạn $[1,d]$)
3.2 Gibbs Sampling là trường hợp đặc biệt của Metropolis-Hastings
Gibbs Sampling có thể xem như là một trường hợp đặc biệt của Metropolis-Hastings như sau:
Đầu tiên chúng ta lặp đi lặp lại $n-1$ lần từ trạng thái khởi tạo $x^0$ để thu được $n$ mẫu. Với mỗi lần lặp chúng ta lại lặp $d$ lần.
Mỗi lần lặp nhỏ trong $d$ lần là mỗi lần chúng ta đưa ra một dự định và cập nhật trạng thái (nhưng không thêm vào tập mẫu cho mãi đến khi lấy được thành phần thứ $d$ của vectơ ngẫu nhiên $x$).
Phân bố dự định mỗi lần lặp con $j$ được cho:
$$ \color{WildStrawberry} q_j(x’|x) = p(x_j’ | \mathbf{x}_{-j}) I(x’_{-j} = x_{-j})$$
Với $I$ là hàm thuộc tính (indicator function), hàm $I$ này đảm bảo trong các bước nhảy con chỉ thành phần thứ $j$ bị thay đổi, các thành phần khác giữ nguyên:
$$ I(x’_{-j}=x_{-j}) = \left\{ { \begin{array}{*{20}{c}}{1}&{\text{nếu } x’_{-j}=x_{-j}}\\ 0 &{\text{còn lại}}\end{array} } \right. $$
Và lúc này xác suất chấp nhận tại mỗi bước nhảy con luôn là $r_j = 1$. Bởi theo xác suất có có điều kiện ta có biến cố $x$ xảy ra là biến cố giao giữa biến cố $x_j$ xuất hiện và $x_{-j}$ xuất hiện đồng thời, nói cách khác lúc này: $p(x) = p(x_j, x_{-j}) = p(x_j | x_{-j}) p(x_{-j})$ do đó lúc này ta có:
$$\alpha_{j} = \frac{p(x’)q(x|x’)}{p(x)q(x’|x)} = \frac{p(x’_{j} | \mathbf{x’}_{-j}) p(\mathbf{x’}_{-j}) p(x_j | \mathbf{x’}_{-j})}{p(x_{j} | \mathbf{x}_{-j}) p(\mathbf{x}_{-j}) p(x’_j | \mathbf{x}_{-j})} $$
Lưu ý là $x$ và $x’$ chỉ khác nhau ở thành phần thứ $j$, hay $ \mathbf{x}_{-j} = \mathbf{x’}_{-j}$ do đó biến cố $\mathbf{x}_{-j}$ và biến cố $\mathbf{x’}_{-j}$ khả năng xảy ra là như nhau! Do đó ta có $p(x’_j | \mathbf{x’}_{-j}) = p(x’_j | \mathbf{x}_{-j})$, $p(x_j | \mathbf{x’}_{-j}) = p(x_j | \mathbf{x}_{-j})$ và $p(\mathbf{x’}_{-j}) = p(\mathbf{x}_{-j})$:
$$\alpha_{j} = \frac{p(x’_{j} | \mathbf{x}_{-j}) p(\mathbf{x}_{-j}) p(x_j | \mathbf{x}_{-j})}{p(x_{j} | \mathbf{x}_{-j}) p(\mathbf{x}_{-j}) p(x’_j | \mathbf{x}_{-j})} = 1$$
Do đó $r_j = \min \{ 1, \alpha\} = 1$. Hay nói cách khác Gibbs Sampling là một trường hợp đặc biệt của Metropolis–Hastings gồm nhiều bước nhảy nhỏ! Mặc dù $r_j = 1$ nhưng không có nghĩa là Gibbs Sampling hội tụ nhanh, bởi vì cứ sau mỗi chu kì cập nhật $d$ chiều thì Gibbs Sampling mới nhận một mẫu.
Gibbs Sampling có thể xem như một trường hợp của Metropolis-Hastings chạy $(n-1)d$ lần để lấy mẫu cứ mỗi $d$ chu kỳ với phân bố dự định dựa trên xác suất có điều kiện của phân bố!
3.3 Ưu khuyết điểm của Gibbs Sampling
Xét về ưu điểm:
- Không cần phải thiết kế tối ưu hàm phân bố dự định quá nhiều.
- Luôn luôn chấp nhận trạng thái dự định mới.
Khuyết điểm:
- Phải lấy được phân bố xác suất có điều kiện.
- Việc tính toán lấy mẫu từ phân bố xác suất có điều kiện tính toán nên phải ít chi phí (vì muốn lấy $n$ mẫu chúng ta phải chạy $(n-1)d$ lần).
4. Tự cài đặt thuật toán
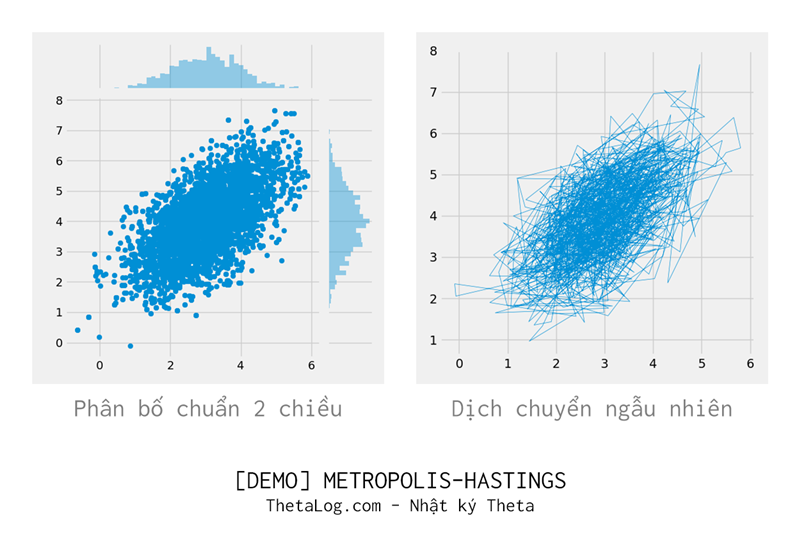
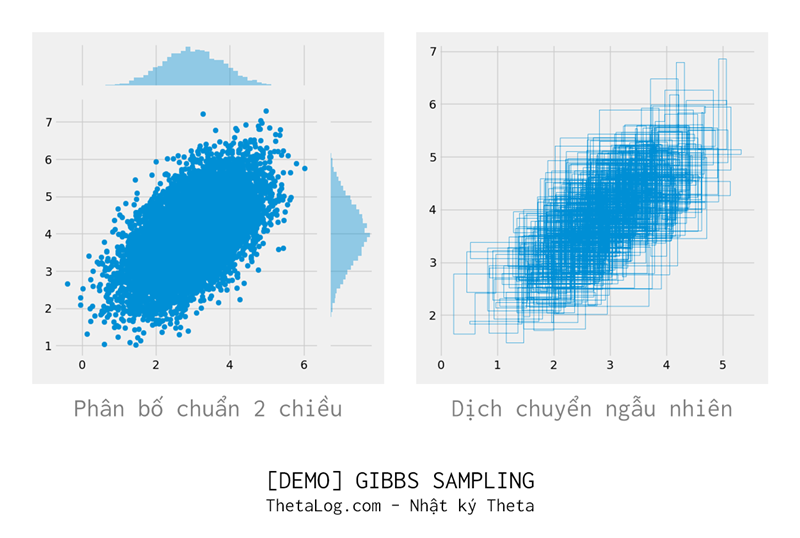
Tất nhiên rất ít ai lại lấy thuật toán này để lấy mẫu phân bố chuẩn (vì phân bố chuẩn có nhiều phương pháp khác hiệu quả hơn), tuy nhiên để tiện tính toán và theo dõi, phần này sẽ trình bày dưới dạng lấy phân bố $p(x)$ là phân bố chuẩn $2$ chiều.
4.1 Metropolis–Hastings
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: Python 3.7.0 (Anaconda) | |
# | > DEMO Thuật toán Metropolis-Hastings | |
# |_____________________________________________________________________|/
import numpy as np # ver 1.15.4
import matplotlib.pyplot as plt # ver 3.0.2
from matplotlib import style
from scipy import stats # 1.1.0
import seaborn as sns # 0.9.0
style.use('fivethirtyeight')
def p_pdf(x):
"""
Hàm mật độ xác suất p(x) của phân bố cần lấy
p(x) = N(x | mean, cov) hay x ~ N(mean, cov)
:param x: np.array - sự kiện x
:return p.d.f: numpy.array - mật độ xác suất x
"""
mean = np.array([3, 4])
cov = np.array([[1.0, 0.7],
[0.7,1.2]])
return stats.multivariate_normal.pdf(x, mean, cov)
def q_pdf(x_proposed, x_current):
"""
Hàm mật độ xác suất của q(x)
q(x' | x) = N(x' | x, cov) hay x' | x ~ N(x, cov)
:param x_proposed: np.array - trạng thái dự định
:param x_current: np.array - trạng thái hiện tại
:return p.d.f: numpy.array - mật độ xác suất x_proposed
"""
cov = np.array([[3.0, 0.],
[0., 3.0]])
return stats.multivariate_normal.pdf(x_proposed, x_current, cov)
def sample_from_q(x_current):
"""
Hàm lấy mẫu từ phân bố dự định q(x) (proposal distribution)
x_current -> x
x_proposed -> x'
Phân bố q() có phân bố chuẩn mean=x, covariance = cov
q(x' | x) = N(x' | x, cov) hay x' | x ~ N(x, cov)
:param x: np.array - trạng thái trước đó
:return x_proposed: numpy.array - trạng thái dự định mới
"""
cov = np.array([[3.0, 0.],
[0., 3.0]])
x_proposed = np.random.multivariate_normal(x_current, cov)
return x_proposed
def metropolis_hastings(p, q, n, q_sampler, init):
"""
Thuật toán Metropolis Hastings
:param p: function - hàm mật độ xác suất p(x)
:param q: function - hàm mật độ xác suất q(x)
:param n: int - số lượng mẫu cần lấy
:param q_sampler: function - hàm lấy mẫu từ q
:param init: numpy.array - vị trí khởi tạo
:return samples: numpy.array 2D - tập mẫu
"""
samples = np.zeros(shape=(n, 2))
samples[0] = init
for i in range(n-1):
x_current = samples[i]
x_proposed = q_sampler(x_current)
# Vì q(x' | x) = q(x | x') nên ta đơn giản tính toán
# alpha = (p(x_proposed) * q(x_current, x_proposed)) / \
# (p(x_current) * q(x_proposed, x_current))
alpha = p(x_proposed) / p(x_current)
r = min(1.0, alpha)
u = np.random.uniform(0.0, 1.0)
if u < r:
samples[i+1] = x_proposed
else:
samples[i+1] = x_current
return samples
if __name__ == '__main__':
init = np.array([3.1, 4.2])
n = 10000
samples = metropolis_hastings(p_pdf, q_pdf, n, sample_from_q, init)
# Vẽ nào
sns.jointplot(samples[:, 0], samples[:, 1])
plt.show()
# Nếu muốn vẽ đường dịch chuyển
plt.plot(samples[:3000, 0], samples[:3000, 1], linewidth=0.5)
plt.show()# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: R version 3.5.0 | |
# | > DEMO Thuật toán Metropolis-Hastings | |
# |_____________________________________________________________________|/
library(mvtnorm)
library(ggplot2)
# Hàm mật độ xác suất p(x) của phân bố cần lấy
# p(x) = N(x | mean, cov) hay x ~ N(mean, cov)
#
# :param x: - sự kiện x
#
# :return p.d.f: - mật độ xác suất x
p_pdf <- function(x) {
mean <- c(3, 4)
cov <- matrix(c(1.0, 0.7, 0.7, 1.2), nrow = 2)
return(dmvnorm(x = x, mean = mean, sigma = cov))
}
# Hàm mật độ xác suất của q(x)
# q(x' | x) = N(x' | x, cov) hay x' | x ~ N(x, cov)
#
# :param x_proposed: - trạng thái dự định
# :param x_current: - trạng thái hiện tại
#
# :return p.d.f: - mật độ xác suất x_proposed
q_pdf <- function(x_proposed, c_current) {
cov <- matrix(c(3.0,0.0,0.0,3.0), nrow = 2)
return(dmvnorm(x = x_proposed, mean = x_current, sigma = cov))
}
# Hàm lấy mẫu từ phân bố dự định q(x) (proposal distribution)
# x_current -> x
# x_proposed -> x'
# Phân bố q() có phân bố chuẩn mean=x, covariance = cov
# q(x' | x) = N(x' | x, cov) hay x' | x ~ N(x, cov)
#
# :param x: - trạng thái trước đó
# :return x_proposed: - trạng thái dự định mới
sample_from_q <- function(x_current) {
cov <- matrix(c(3.0,0.0,0.0,3.0), nrow = 2)
x_proposed <- rmvnorm(n = 1, mean = x_current, sigma = cov)
return(x_proposed)
}
# Thuật toán Metropolis Hastings
#
# :param p: - hàm mật độ xác suất p(x)
# :param q: - hàm mật độ xác suất q(x)
# :param n: - số lượng mẫu cần lấy
# :param q_sampler: - hàm lấy mẫu từ q
# :param init: - vị trí khởi tạo
#
# :return samples: 2D - tập mẫu
metropolis_hastings <- function(p, q, n, q_sampler, init) {
samples <- data.frame(matrix(init, nrow = 1, byrow = TRUE))
for (i in 1:(n-1)){
x_current <- as.numeric(tail(samples, n = 1))
names(x_current) <- colnames(samples)
x_proposed <- q_sampler(x_current)
alpha = p(x_proposed) / p(x_current)
r <- min(1, alpha)
u <- runif(1, 0.0, 1.0)
if (u < r){
names(x_proposed) <- colnames(samples)
samples <- rbind(samples, x_proposed)
}
else {
names(x_current) <- colnames(samples)
samples <- rbind(samples, x_current)
}
}
return(samples)
}
# Điểm khởi tạo
init <- c(3.1, 4.2)
# Số lượng điểm
n <- 10000
samples <- metropolis_hastings(p_pdf, q_pdf, n, sample_from_q, init)
# Vẽ
ggplot(data=samples,aes(x=X1, y=X2)) + geom_point()4.2 Gibbs Sampling
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: Python 3.7.0 (Anaconda) | |
# | > DEMO Thuật toán Gibbs Sampling | |
# |_____________________________________________________________________|/
import numpy as np # ver 1.15.4
import matplotlib.pyplot as plt # ver 3.0.2
from matplotlib import style
from scipy import stats # 1.1.0
import seaborn as sns # 0.9.0
style.use('fivethirtyeight')
def q_x_given_y(y, mean_p, cov_p):
"""
Phân bố xác suất có điều kiện
q(x | y) phân bố dự định đầu tiên
Tìm hiểu thêm về phân bố xác suất có điều kiện phân bố chuẩn
http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7c_gaussian_processes.html
:param y: float - điều kiện đã biết
:param mean_p: np.array - kỳ vọng phân bố chuẩn p
:param cov_p: np.array - hiệp phương sai phân bố chuẩn p
:return proposed_state: numpy.array - trạngt thái mới
"""
muy = mean_p[0] + cov_p[1, 0] / cov_p[0, 0] * (y - mean_p[1])
sigma = cov_p[0, 0] - cov_p[1, 0] / cov_p[1, 1] * cov_p[1, 0]
proposed_state = np.random.normal(muy, sigma)
return proposed_state
def q_y_given_x(x, mean_p, cov_p):
"""
Phân bố xác suất có điều kiện
q(y | x) phân bố dự định thứ hai
Tìm hiểu thêm về phân bố xác suất có điều kiện phân bố chuẩn
http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7c_gaussian_processes.html
:param x: float - điều kiện đã biết
:param mean_p: np.array - kỳ vọng phân bố chuẩn p
:param cov_p: np.array - hiệp phương sai phân bố chuẩn p
:return proposed_state: numpy.array - trạng thái mới
"""
muy = mean_p[1] + cov_p[0, 1] / cov_p[1, 1] * (x - mean_p[0])
sigma = cov_p[1, 1] - cov_p[0, 1] / cov_p[0, 0] * cov_p[0, 1]
proposed_state = np.random.normal(muy, sigma)
return proposed_state
def gibbs_sampling_2d_normal_distribution(mean_p, cov_p, n, init):
"""
Lấy mẫu Gibbs Sampling
:param mean_p: np.array - kỳ vọng phân bố chuẩn p
:param cov_p: np.array - hiệp phương sai phân bố chuẩn p
:param n: int - lượng mẫu cần lấy
:param init: np.array - điểm khởi tạo
"""
samples = np.zeros(shape=(n, 2))
random_walk = np.zeros(shape=(n*2, 2))
samples[0] = init
random_walk[0] = init
for i in range(n-1):
y = samples[i, 1]
x = q_x_given_y(y, mean_p, cov_p)
samples[i+1, :] = np.array([x, y])
random_walk[2*i+1, :] = np.array([x, y])
y = q_y_given_x(x, mean_p, cov_p)
samples[i+1, :] = [x, y]
random_walk[2*i+2, :] = np.array([x, y])
return samples, random_walk
if __name__ == '__main__':
n = 10000
init = np.array([2, 2.5])
mean_p = np.array([3, 4])
cov_p = np.array([[1.0, 0.7],
[0.7,1.2]])
samples, random_walk = gibbs_sampling_2d_normal_distribution(mean_p, cov_p, n, init)
# Vẽ nào
sns.jointplot(samples[:, 0], samples[:, 1])
plt.show()
# Nếu muốn vẽ đường dịch chuyển
plt.plot(random_walk[:2000, 0], random_walk[:2000, 1], linewidth=0.5)
plt.show()
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: R version 3.5.0 | |
# | > DEMO Gibbs Sampling | |
# |_____________________________________________________________________|/
library(ggplot2)
# Phân bố xác suất có điều kiện
# q(x | y) phân bố dự định đầu tiên
#
# Tìm hiểu thêm về phân bố xác suất có điều kiện phân bố chuẩn
# http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7c_gaussian_processes.html
#
# :param y: - điều kiện đã biết
# :param mean_p: - kỳ vọng phân bố chuẩn p
# :param cov_p: - hiệp phương sai phân bố chuẩn p
#
# :return proposed_state: - trạngt thái mới
q_x_given_y <- function(y, mean_p, cov_p){
muy <- mean_p[1] + cov_p[[2, 1]] / cov_p[[1, 1]] * (y - mean_p[2])
sigma <- cov_p[1, 1] - cov_p[2, 1] / cov_p[2, 2] * cov_p[2, 1]
proposed_state <- rnorm(1, mean = muy, sd = sigma)
return(proposed_state)
}
# Phân bố xác suất có điều kiện
# q(y | x) phân bố dự định thứ hai
#
# Tìm hiểu thêm về phân bố xác suất có điều kiện phân bố chuẩn
# http://www.inf.ed.ac.uk/teaching/courses/mlpr/2017/notes/w7c_gaussian_processes.html
#
# :param x: - điều kiện đã biết
# :param mean_p: - kỳ vọng phân bố chuẩn p
# :param cov_p: - hiệp phương sai phân bố chuẩn p
#
# :return proposed_state: - trạng thái mới
q_y_given_x <- function(x, mean_p, cov_p){
muy <- mean_p[2] + cov_p[[1, 2]] / cov_p[[2, 2]] * (x - mean_p[1])
sigma <- cov_p[2, 2] - cov_p[1, 2] / cov_p[1, 1] * cov_p[1, 2]
proposed_state <- rnorm(1, mean = muy, sd = sigma)
return(proposed_state)
}
# Lấy mẫu Gibbs Sampling
#
# :param mean_p: - kỳ vọng phân bố chuẩn p
# :param cov_p: - hiệp phương sai phân bố chuẩn p
# :param n: - lượng mẫu cần lấy
# :param init: - điểm khởi tạo
#
# :return samples: tập mẫu phân bố nhiều chiều
gibbs_sampling_2d_normal_distribution <- function(mean_p, cov_p, n, init){
samples <- data.frame(matrix(init, nrow = 1, byrow = TRUE))
for (i in 1:(n-1)){
y <- tail(samples, n = 1)[[1]]
x <- q_x_given_y(y, mean_p, cov_p)
y <- q_y_given_x(x, mean_p, cov_p)
new_x <- c(x, y)
names(new_x) <- colnames(samples)
samples <- rbind(samples, new_x)
}
return(samples)
}
# Điểm khởi tạo
init <- c(2, 2.5)
# Số lượng điểm
n <- 10000
mean_p <- c(3,4)
cov_p <- matrix(c(1.0,0.7,0.7,1.2), nrow = 2)
samples <- gibbs_sampling_2d_normal_distribution(mean_p, cov_p, n, init)
# Vẽ
ggplot(data=samples,aes(x=X1, y=X2)) + geom_point()
5. Ứng dụng
Metropolis–Hastings & Gibbs Sampling có rất nhiều ứng dụng, dưới đây là một vài ứng dụng tiêu biểu:
- Lấy thêm dữ liệu huấn luyện (Data Augmentation): việc lấy thêm dữ liệu để xây dựng mô hình đôi lúc cần thiết khi lượng dữ liệu thu thập được không đủ để xây dựng một mô hình tốt. (tuy nhiên việc này đòi hỏi bạn phải am hiểu mô hình mình đang xử lí)
- Suy luận tham số mô hình (Inferring Parameters): một số mô hình học máy, xác suất thống kê có thể nhờ vào việc lấy mẫu để giúp suy luận ra tham số. Ví dụ Gibbs Sampling giúp suy ra tham số Latent Dirichlet Allocation, Gaussian Mixture Model,…
- Kiểm tra mô hình (Model checking): mô hình đã xây dựng với dữ liệu bạn đầu, bạn muốn kiểm tra xem nó chạy đúng với những giả định của mình hay không, tạo ra dữ liệu và kiểm tra có vẻ không phải là một ý tồi nhỉ.
- Phục vụ nghiên cứu (Research Design): bạn xây dựng một mô hình rất phức tạp, bạn tính toán một số tham số dựa trên mô hình lý thuyết, tuy nhiên bạn lại không dám chắc rằng nó đúng, tại sao không thiết kế một mô hình kiểm tra qua thực nghiệm nhỉ?
Một vài ứng dụng thú vị bạn đọc có thể tìm hiểu thêm:
- Giải mã với MCMC, giải bài toán Knapsack: Tại đây
- Khử nhiễu ảnh với Gibbs sampling với mô hình Ising Tại đây
- Tính tích phân một số hàm phức tạp Tại đây
- Ứng dụng sinh học vào bài toán Motif-finding: Tại đây
6. Phần đọc thêm
Nếu như bạn thích thú với các kỹ thuật MCMC thì có lẽ bạn không nên bỏ qua $2$ thuật toán sau:
- Hamiltonian Monte Carlo (viết tắt HMC): https://arxiv.org/abs/1701.02434
- No-U-Turn Sampler (viết tắt NUTS): https://arxiv.org/abs/1111.4246
Thường thì không nên tự cài đặt những thuật toán này, có rất nhiều phần mềm, thư viện phát triễn mạnh mẽ:
- Stan: https://mc-stan.org/
- PyMC3: https://docs.pymc.io/
- JAGS - Just Another Gibbs Sampler: http://mcmc-jags.sourceforge.net/
- OpenBUGS: http://www.openbugs.net/
7. Phần kết
Metropolis–Hastings và Gibbs Sampling là $2$ thuật toán thuộc nhóm Markov Chain Monte Carlo (MCMC) thường dùng để lấy mẫu một phân bố bất kì dựa trên việc gieo điểm ngẫu nhiên và dịch chuyển sang các trạng thái dự định được xem là hợp lí. Thuật toán có nhiều ứng dụng để giải quyết nhiều loại bài toán khác nhau.
Chúc bạn có những giây phút vui vẻ bên thuật toán!
Tham khảo
- Christophe Aandrieu, Nando De Freitas, Arnaud Doucet, Michael I. Jordan. An Introduction to MCMC for Machine Learning. https://www.cs.ubc.ca/~arnaud/andrieu_defreitas_doucet_jordan_intromontecarlomachinelearning.pdf
- Stefano Ermon, ErmonGroup. Metropolis-hastings Recap of Markov chains. Stanford CS323. https://ermongroup.github.io/cs323-notes/probabilistic/mh/
- Stefano Ermon, ErmonGroup. Gibbs sampling Sampling and inference tasks. Stanford CS323. https://ermongroup.github.io/cs323-notes/probabilistic/gibbs/
- Iain Murray. Monte Carlo Inference Methods. https://media.nips.cc/Conferences/2015/tutorialslides/nips-2015-monte-carlo-tutorial.pdf
- Kevin P. Murphy. Machine Learning A Probabilistic Perspective. ISBN 978-0-262-01802-9.
- SIAM - Society for Industrial and Applied Mathematics. The Best of the 20th Century: Editors Name Top 10 Algorithms. https://archive.siam.org/news/news.php?id=637
- Christian Robert, George Casella. A Short History of Markov Chain Monte Carlo: Subjective Recollections from Incomplete Data. arXiv:0808.2902. https://arxiv.org/abs/0808.2902
- Wikipedia contributors. “Monte Carlo method.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 17 Dec. 2018. Web. 30 Dec. 2018.
- Dustin Stansbury. MCMC: The Metropolis-Hastings Sampler. https://theclevermachine.wordpress.com/2012/10/20/mcmc-the-metropolis-hastings-sampler/
- MLWhiz. Behold the power of MCMC. https://mlwhiz.com/blog/2015/08/21/mcmc_algorithm_cryptography/