Entropy, Cross Entropy, KL Divergence

Đăng trên bởi Lê Quang Tiến 19 phút trôi qua :D
Nội dung bài viết

Lý thuyết thông tin (Information Theory) là một nhánh toán ứng dụng quan tâm đến các vấn đề định lượng (quantification), lưu trữ (storage) và truyền thông (communication) của thông tin. Thông tin là một khái niệm trừu tượng (không phải một thực thể lý tính) do đó thật khó để định lượng thông tin theo cách thông thường. Trong bài viết này, nội dung hướng đến cách định lượng thông tin, các độ đo thông tin Entropy, Cross Entropy, Kullback–Leibler divergence, mối quan hệ của chúng và một số ứng dụng của những độ đo này.

Nguồn Khan Academy

Lý thuyết thông tin được khởi xướng bởi Claude E. Shannon vào năm 1948 với bài báo khoa học có tiêu đề “A Mathematical Theory of Communication” đặt nền móng nghiên cứu nền tảng về các giới hạn liên quan đến xử lí tín hiệu (signal processing) và các thao tác truyền thông (communication operations) như nén dữ liệu. Phần lớn ứng dụng của lý thuyết thông tin thường liên quan đến việc nén dữ liệu (ZIP, MP3, JPEG,…) và mã hóa kênh (truyền dữ liệu số qua đường dây điện thoại,…).

Thoạt nghe qua thì có vẻ như lý thuyết thông tin chẳng liên quan gì đến thống kê và học máy nhưng thực tế lại có một sự kết nối sâu xa! Độ đo Entropy, Cross Entropy, Kullback–Leibler divergence là những độ đo được sử dụng rất nhiều trong học máy dùng để huấn luyện các bộ phân lớp, vì sao vậy? Chúng ta sẽ đi tìm câu trả lời ngay sau đây!

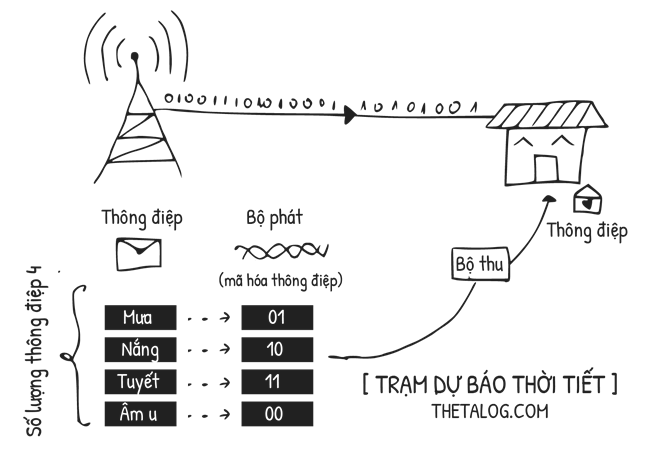
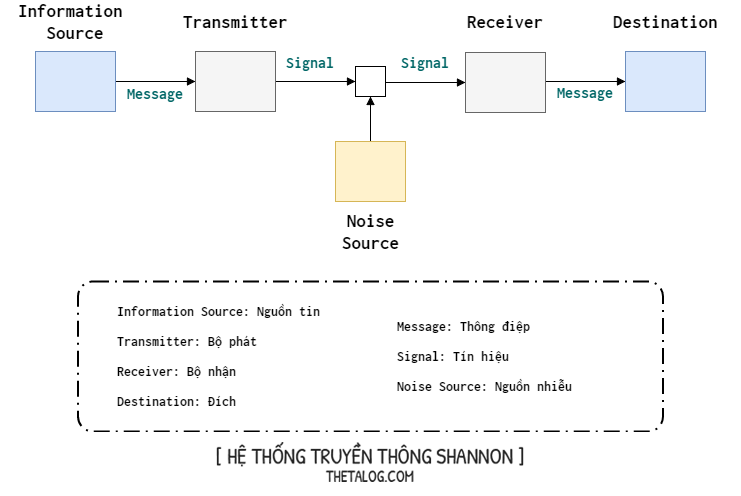
Biểu đồ phía trên được gọi là hệ thống truyền thông (Shannon communication system) nằm trong bài báo nổi tiếng “A Mathematical Theory of Communication”:

  • Nguồn tin: nơi tạo ra thông điệp và gửi cho bộ phát.
  • Bộ phát: nhận thông điệp và tạo ra một tín hiệu (digital, analog) để gửi qua kênh truyền thông tin.
  • Kênh: là nơi mang tín hiệu từ bộ phát và gửi đến bộ thu.
  • Nhiễu: trong quá trình truyền đi tín hiệu, nguồn gây ra nhiễu làm sai lệch tín hiệu gửi đi.
  • Bộ thu: nhận tín hiệu và biến đổi thành thông điệp mới gửi đến đích.
  • Đích: có thể là người hoặc máy mà thông điệp được chỉ định gửi đến.

Mục tiêu của một hệ thống truyền thông là truyền tải những thông điệp đáng tin cậy và hiệu quả từ người gửi đến người nhận.

The fundamental problem of communication is that of reproducing at one point, either exactly or approximately, a message selected at another point.
— Claude E. Shannon

Nếu như thông điệp nằm trong một tập hữu hạn sự lựa chọn truyền thông mà nguồn và đích có thể giao tiếp được (với mọi sự lựa chọn là như nhau) thì khi đó số lượng thông điệp hoặc bất kì hàm đơn điệu nào của nó có thể được xem xét như một độ đo thông tin tái sản sinh thông điệp được chọn từ tập trước đó. Claude E. Shannon cho rằng một trong những hàm toán học phù hợp với nhất với việc này là hàm logarit.

Sự lựa cơ số cho hàm logarit phụ thuộc vào đơn vị đo lường thông tin. Nếu như cơ số được chọn là $2$ thì đơn vị đo là bits thông tin (binary digits), đôi lúc cũng có tài liệu gọi đơn vị thông tin khi sử dụng cơ số $2$ là shannon, nếu như cơ số là $ e \approx 2,71828182846…$ hay nói cách khác hàm sử dụng là hàm logarit tự nhiên thì đơn vị thông tin là nats (dựa trên tên gọi natural logarithm), nếu như cơ số là $10$ thì đơn vị thông tin là hartley (còn hay gọi dit hoặc ban).

Trong kỷ nguyên số, bộ phát mã hóa thông điệp dưới dạng dãy bits và gửi qua kênh truyền đến bộ thu. Bit viết tắt của Binary digIT, được gọi là đơn vị đo lường thông tin. Một bit có thể nhận một trong hai giá trị: $0$ hoặc $1$. Dể dàng nhận ra rằng một bit biểu diễn cho hai sự lựa chọn.

Xét bài toán đơn giản sau đây, một trạm dự báo thời tiết gửi thông điệp đến các hộ gia đình về tình hình thời tiết địa phương:

  • Thông điệp: tập thông điệp là $\{ \text{mưa}, \text{nắng}, \text{tuyết}, \text{âm u} \}$ mà nơi gởi và đích đến có thể giao tiếp được với nhau. Giả định rằng xác suất xảy ra mưa, nắng, tuyết, âm u là như nhau.
  • Bộ phát và bộ thu mã hóa và giải mã nhị phân.

Với mục đích truyền thông như trên, thì lượng đơn vị thông tin cần dùng là:$$\log_{2}(4) = 2 \text{ (bits)}$$Với $2 \text{ bits}$ là giá trị $ \text{bits}$ định lượng thông tin cho mục đích truyền thông mô tả phía trên.
Một câu hỏi được đặt ra: bạn có thể gửi một tấm ảnh $200 \text{ KB}$ hoặc gửi một chuổi kí tự “rainy”, “sunny”, “snowy”, “gloomy” để phục vụ mục đích truyền thông như trên thì giá trị định lượng thông tin có thay đổi không?
Thực tế thì bạn có thể gửi bao nhiêu dữ liệu cũng được, nhưng số lượng $\text{bits}$ ít nhất để bạn truyền thông điệp trên chắc chắn là $2 \text{ bits}$. Và vì mục đích truyền thông là truyền tải thông điệp từ nơi gửi đến nơi nhận, nếu như ta không quan tâm đến “thông tin thừa” phát sinh (phần thông tin dôi ra) thì giá trị định lượng thông tin cho mục tiêu trên chỉ có $2 \text{ bits}$ là bits thông tin.


Nhưng nếu như mỗi thông điệp “khả năng xảy ra” không như nhau mà dưới một xác suất thì sao?

Trước khi bàn luận về độ đo Entropy thì mình muốn giới thiệu với các bạn về độ đo self-information để định lượng thông tin của một thông điệp có xác suất xảy ra $p$. Độ đo hàm lượng thông tin được định nghĩa như sau:

Hàm lượng thông tin (Self-information)
Độ đo hàm lượng thông tin của một thông điệp với một biến cố $E$ là: $$\text{I}(E) = \log_{b}\frac{1}{\Pr(E)}$$Với $b$ là cơ số phụ thuộc vào đơn vị thông tin.
Một cách cảm tính, nếu như thông điệp gắn liền với một biến cố chắc chắn xảy ra (xác suất $p=1$) chẳng hạn như sa mạc Sahara luôn nắng (giả định rằng xác suất Sahara nắng quanh năm $p=1$), nếu như bạn đã biết thông tin này từ trước, thì việc truyền thông có mang lại lượng thông tin nào cho bạn không?

Mình đang ở sa mạc Sahara và gửi một thông điệp qua email cho bạn rằng: “chào cậu, hôm nay trời nắng đấy!”. Thông điệp này ắt hẳn chẳng mang một chút thông tin nào cho bạn cả! Bởi vì như Sahara lúc hầu như lúc nào chẳng nắng?

Nó dẫn đến ý tưởng xây dựng độ đo hàm lượng thông tin như sau $\text{I}(E)$ như sau:

  • Hàm này phải phụ thuộc vào xác suất xảy ra của biến cố $E$ hay nói cách khác $\text{I}(E) =f(\Pr(E))$ với $f(.)$ là hàm mà chúng ta cần tìm. Nếu như xác suất $\Pr(E) = 1$ thì $I(E) = 0$, nếu như $\Pr(E) <1$ thì $\text{I}(E) > 0$.
  • $\text{I}(E)$ phải là một độ đo không âm, nghịch biến với $\Pr(E)$ khi $\Pr(E)$ càng tăng thì hàm lượng thông tin càng giảm $\text{I}(E)$. Nếu như một sự kiện xảy ra thường xuyên trong cuộc sống, khi nó tiếp tục xảy ra, thì chẳng có gì bất ngờ cả (ít thông tin). Tuy nhiên nếu sự kiện không chắc chắn xảy ra, nhưng lại xảy ra thì chắc chắn thông điệp mang lại một lượng thông tin lớn (nhiều thông tin).
  • Nếu như $A$ và $B$ là hai biến cố độc lập, gọi $C = A \cap B$, ta có $\Pr(A \cap B) = \Pr(A)\Pr(B)$ thì $\text{I}( C) = \text{I}(A) +\text{I}(B)$. Tính chất trên được gọi là thông tin dựa trên các biến cố độc lập mang tính chất cộng tính. Đây là tính chất quan trọng nhất!

Để phần nào hiểu tại sao thông tin cần tính chất cộng tính khi các biến cố độc lập là một tính chất quan trọng, chúng ta có thể xét ví dụ sau đây: Tung đồng xu lên hai lần, gọi $A$ là biến cố lần tung thứ nhất là mặt ngửa, gọi $B$ là biến cố lần tung thứ hai là mặt ngửa, rõ ràng $A$ và $B$ là hai biến cố độc lập, gọi $C= A \cap B$ hay nói cách khác $C$ là biến cố tung hai lần đều là ngửa, nếu thông điệp là $C$ thì rõ ràng thông tin mà bạn có là “A xảy ra” và “B xảy ra” như vậy nếu có một độ đo thông tin phù hợp thì nó phải thỏa tính chất cộng tính như trên.

Thế $f(.)$ vào tính chất cuối cùng ta có: $$ f(\Pr( C)) = f(\Pr(A)) + f(\Pr(B))$$ Mà ta biết rằng $\Pr( C) = \Pr(A)\Pr(B)$ nên lúc này $$ f(\Pr(A) \Pr(B)) = f(\Pr(A)) + f(\Pr(B))$$ Đặt $x = \Pr(A)$ và $y = \Pr(B)$ viết gọn lại $$ f(x.y) = f(x) + f(y)$$

Lớp các hàm thỏa mãn điều trên có dạng: $f(x) = K \cdot \ln x$. Lưu ý là do phải thỏa mãn hai điều kiện đầu, từ khi xác suất luôn là một số luôn nằm trong đoạn $0$ đến $1$ và thông tin của một biến cố phải không âm, do đó $K<0$. Ngoài ra $K$ đóng một vai trò quan trọng nữa là điều chỉnh cơ số hàm logarit vì $\log_{b} x = \ln x / ln b$. Từ những lập luận như trên ta thu được công thức hàm lượng thông tin của một biến cố.

Shannon phát hiện ra hàm phù hợp để định lượng thông tin và đặc biệt thỏa tính chất cộng tính thông tin với các biến cố độc lập là hàm logarit (nó thỏa mãn một số vấn đề về toán học, tuy nhiên không hẳn là hoàn toàn, trong bài báo A Mathematical Theory of Communication có đề ra 3 quan điểm để chọn hàm logarit làm độ đo thông tin, một trong các quan điểm là “một cách trực giác thì dường như nó là một độ đo thích hợp”, đây cũng là một yếu tố quan trọng nhất của người làm khoa học, khoa học đi từ nhận thức cảm tính qua nhiều bậc thang trừu xuất mới đi đến định nghĩa hình thức, trực giác của người làm khoa học rất quan trọng).

Trước khi đến với nội dung các độ đo thông tin khác chúng ta thống nhất một số vấn đề như sau:

  • Thông tin có thể định lượng được bằng một đơn vị thông tin (bits, nats,…)
  • Nếu như thông điệp nằm trong một tập thông điệp với khả năng xảy ra là như nhau thì lượng thông tin của thông điệp là $\log_{b} N$ với $N$ là số lượng thông điệp và $b$ là cơ số của đơn vị thông tin sử dụng.
  • Nếu như thông điệp nằm trong một tập thông điệp, mà thông điệp có xác suất xảy ra là $p$ thì lượng thông tin của thông điệp là $\log_{b}\left(1/p \right)$. Lưu ý là $N=1/p$ có thể diễn giải là số lượng thông điệp mà nguồn tin phát sinh cứ $N$ thông điệp thì phát sinh $1$ thông điệp mà ta đang xét, do đó thông điệp có xác suất $1/p$.
  • Tính chất của thông tin: thông tin càng nhiều (càng bất ngờ) là những sự kiện càng ít xảy ra, thông tin càng ít (càng hiển nhiên) là những sự kiện xảy ra thường xuyên.

1. Entropy

Entropy xuất hiện lần đầu tiên trong cơ học thống kê (Boltzmann Entropy), Shannon ban đầu tìm ra Entropy và đặt tên nó là “độ bất xác định” (Uncertainty thay vì Entropy), cuối cùng với lời khuyên của John Von Neumann cái tên này được giữ lại.

Về bản chất Entropy chính là trung bình thông tin của biến ngẫu nhiên rời rạc!

Entropy
Với biến ngẫu nhiên rời rạc $X$ nhận các giá trị $ \left\{ x_{1},...,x_{n} \right\} $ và hàm khối xác suất pmf (probability mass function) $\Pr(X)$ thì Entropy của $X$ là:$$\text{H}(X) = \mathbb{E}(\text{I}(X)) = \sum_{i=1}^{n}\Pr(x_{i})\text{I}(x_{i})=\sum_{i=1}^{n}\Pr(x_{i}) \log_{b}\frac{1}{\Pr(x_{i})}$$ Hay nói cách khác: $$\text{H}(X) = - \sum_{i=1}^{n}\Pr(x_{i}) \log_{b}\Pr(x_{i})$$ Với $b$ là cơ số được chọn dựa trên đơn vị thông tin sử dụng. Entropy thông tin (còn gọi Entropy nhị phân) là hàm Entropy với cơ số $b=2$.

Đôi lúc để ký hiệu tiện lợi và dể nhìn hơn chúng ta có thể viết Entropy với vector xác suất $p = (p_{i},...p_{n})$ với $p_{i} = \Pr(X=x_{i})$ khi đó $\text{H}(p)$: $$\text{H}(p) = - \sum_{i=1}^{n} p_{i} \log_{b}p_{i}$$

Nhìn vào công thức trên bạn sẽ nhận ra một điều không đúng! Đó chính là $\log_{b}(0)$ không xác định. Tuy nhiên chúng ta lại có tính chất sau của giới hạn hàm số $-x \log_{b}x$ với $b$ là cơ số cho trước:

$$\lim_{x \to 0} -x\cdot \log_{b} x = 0$$

Chúng ta có thể chứng minh bằng quy tắc L’Hospital với $f(x) = \log_{b} x$ và $g(x) = 1 / x$ như sau:

$$\lim_{x \to 0} -x\cdot \log_{b} x = - \lim_{x \to 0} \frac{\log_{b} x}{1 / x} = - \lim_{x \to 0} \frac{f(x)}{g(x)}= - \lim_{x \to 0} \frac{f’(x)}{g’(x)} $$

$$ = - \lim_{x \to 0} \frac{1/ (x\cdot \ln b)}{-1 / x^{2}} = \lim_{x \to 0} \frac{x^{2}}{x\cdot \ln b} = \lim_{x \to 0} \frac{x}{\ln b} = 0 $$

Vì thế với các trường hợp xác suất bằng $0$ hàm $\log$ không xác định thì qui ước rằng $0 \log_{b} 0 = 0$ (hãy lưu ý việc này trong lập trình tính toán).

Một vài tính chất quan trọng của Entropy:

  • Hàm entropy là một hàm không âm $\text{H}(X) \ge 0$ dấu bằng xảy ra khi và chỉ khi $p_{i} = 0$ với một $i$ nào đó.
  • Hàm Entropy cực đại khi phân bố xác suất là phân bố đều, với $\text{H} (X) \le \log_{b} (n)$ dấu bằng xảy ra khi và chỉ khi $p_{i} = \Pr(X=x_{i}) = \frac{1}{n}$ với mọi $i$.

Entropy là độ đo bất xác định khi dự đoán trạng thái của một biến ngẫu nhiên $X$. Entropy thông tin của biến ngẫu nhiên $X$ càng cao (càng nhiều thông tin chứa trong thông điệp) thì càng khó dự đoán.

Giả sử rằng có 4 chiếc hộp đen như trên hình, bạn biết trước trong hộp gồm có những gì! Theo bạn hộp nào dể dự đoán hơn hộp nào?

    Gọi $p_{1}$ là xác suất bóc lấy ra hình vuông, $p_{2}$ là xác suất lấy ra hình tròn. Với vector $p = (p_{1}, p_{2})$
  • Trường hợp 1: với $4$ hình vuông $(p_{1} = 1.00)$, $0$ hình tròn $(p_{2} = 0.00)$
  • Trường hợp 2: với $3$ hình vuông $(p_{1} = 0.75)$, $1$ hình tròn $(p_{2} = 0.25)$
  • Trường hợp 3: với $2$ hình vuông $(p_{1} = 0.50)$, $2$ hình tròn $(p_{2} = 0.50)$
  • Trường hợp 4: với $2$ hình vuông $(p_{1} = 0.40)$, $3$ hình tròn $(p_{2} = 0.60)$
Tạm thời chúng ta không bàn đến toán học! Cảm tính trước nhé:
  • Trường hợp 1: chẳng có gì để phải dự đoán cả, chắc chắn là vuông rồi.
  • Trường hợp 2: không khó dự đoán lắm, vuông nhiều thế cơ mà.
  • Trường hợp 3: khó quá, ai mà đoán được ra gì. Hỗn loạn thế kia!
  • Trường hợp 4: khó dự đoán đấy, tuy nhiên vẫn dể hơn hộp 3.
Sắp xếp theo thứ tự dự đoán từ dể đến khó: 1, 2, 4, 3.
Thử với Entropy thông tin nào:
  • Trường hợp 1: $\text{H}(p) = -1.00 \cdot \log_{2}(1.00) - 0.00 \cdot \log_{2}(0.00) = 0$
  • Trường hợp 2: $\text{H}(p) = -0.75 \cdot \log_{2}(0.75) - 0.25 \cdot \log_{2}(0.25) \approx 0.811$
  • Trường hợp 3: $\text{H}(p) = -0.50 \cdot \log_{2}(0.50) - 0.50 \cdot \log_{2}(0.50) = 1$
  • Trường hợp 4: $\text{H}(p) = -0.40 \cdot \log_{2}(0.40) - 0.60 \cdot \log_{2}(0.60) \approx 0.970$
Kiểm tra lại dự đoán ban đầu của bạn xem nào!


Bây giờ bạn có thể tự trả lời những câu hỏi sau rồi đấy:

  • Điều gì khiến bạn thấy khó dự đoán người mà mình gặp 11 sáng mai là nam hay nữ? (giả định rằng cứ 11 giờ bạn gặp một người nào đó nhé). Vì Entropy cao.
  • Điều gì khiến bạn thấy mình như một nhà tiên tri và có thể đoán Sahara hôm nay trời nắng dù chẳng cần phải xem bản tin dự báo thời tiết? (giả định rằng xác suất trời nắng gần bằng $1$ và các loại thời tiết khác chiếm một phần nhỏ). Vì Entropy thấp.

Entropy cũng là một độ đo quan trọng trong học máy, trong thuật toán như cây quyết định (decision tree ID3 - Iterative Dichotomiser 3) thì Entropy đóng vai trò nồng cốt, đến đây có lẽ bạn cũng đã hiểu tại sao ID3 luôn chọn giá trị entropy nhỏ nhất.

2. Cross Entropy

Cross Entropy là độ đo giữa hai phân bố $p$ (phân bố đúng - true distribution) và $q$ (phân bố hiện tại) để đo lượng trung bình thông tin khi dùng mã hóa thông tin của phân bố $q$ thay cho mã hóa thông tin phân bố $p$. Cross Entropy cực kì hữu ích trong học máy thống kê, nó thường dùng để làm hàm mất mát (Loss Function) trong các mô hình học máy.

Cross Entropy
Với hai phân bố xác suất rời rạc $P$ và $Q$ và vector xác suất tương ứng của phân bố $p=(p_{1},..., p_{n})$ và $q=(q_{1},..., q_{n})$, độ đo Cross Entropy được định nghĩa như sau:$$H(p,q) = - \sum_{i=1}^{n}p_{i} \log_{b}q_{i}$$

Một số tính chất của độ đo Cross Entropy:

  • Cross Entropy dùng $q$ để mã hóa $p$ luôn luôn lớn hơn hoặc bằng Entropy của $p$ hay nói cách khác $\text{H}(p, q) \ge \text{H}(p)$. Để chứng minh Cross Entropy luôn luôn lớn hơn Entropy bạn có thể dùng một trong ba bất đẳng thức sau: Gibbs’ inequality, Log sum inequality, Jensen’s inequality. (hai bất đẳng thức đầu có thể dùng bất đẳng thức Jensen chứng minh lại, bài này chứng minh không khó nhưng cần lưu ý việc nhập nhằng của hàm logarit không xác định tại $0$). Khi $q_{i} = p_{i}$ với $\forall i$ thì dấu bằng xảy ra Cross Entropy bằng với Entropy hay nói cách khác $\text{H}(p, q) = \text{H}(p)$.

  • Cross Entropy không có tính đối xứng $\text{H} (p,q) \ne \text{H} (q,p)$ nên nó không phải là một khoảng cách mêtric. Trong các bài toán thì độ đọ $\text{H} (p,q)$ thường được dùng với $p$ là phân bố đùng cần dự đoán, phân bố $q$ là phân bố mà mô hình hiện tại đang dự đoán, tối tiểu hàm này để cải thiện mô hình.

  • Cross Entropy khi dùng như hàm mất mát, hàm này phạt rất nặng khi xác suất $p_{i}$ lớn nhưng $q_{i}$ lại nhỏ, lý do là do hàm $-\log_{b} (x)$ tăng rất nhanh khi $x$ càng nhỏ và tiến về $0$.

Cross Entropy tiếp tục vẫn là một độ đo sử dụng rất phổ biến trong máy học thống kê, hồi quy logistic (Logistic Regression) sử dụng hàm Cross Entropy để làm hàm mất mát, đôi khi người ta gọi độ đo này là logistic loss, log loss (thư viện scikit-learn dùng tên gọi này).

3. Kullback–Leibler divergence

Trong thống kê và lý thuyết thông tin, độ đo Kullback–Leibler divergence (còn hay gọi là Entropy tương đối, viết tắt KL divergence) là một độ đo đi đo mức độ lệch của một phân bố đối với phân bố được chỉ định. Kullback–Leibler divergence được khởi xướng bởi Solomon Kullback và Richard Leibler vào năm 1951 như một độ đo lệch có định hướng giữa phân bố kỳ vọng so với một phân bố khác. Kullback thích gọi đây là thông tin phân biệt (discrimination information).

Nói một cách đơn giản, KL divergence là độ đo sự khác nhau giữa hai phân bố xác suất. Nói theo ngôn ngữ lý thuyết thông tin, nó đo lượng trung bình thông tin thêm vào nếu chúng ta dùng mã hóa thông tin của phân bố $q$ thay cho mã hóa thông tin phân bố $p$. Định nghĩa của độ đo được cho như sau:

Kullback–Leibler divergence
Với hai phân bố xác suất rời rạc $P$ và $Q$ và vector xác suất tương ứng của phân bố $p=(p_{1},..., p_{n})$ và $q=(q_{1},..., q_{n})$ của biến ngẫu nhiên rời rạc $X$ nhận các giá trị $ \left\{ x_{1},...,x_{n} \right\} $, độ đo Kullback–Leibler divergence được tính:$$ D_{\text{KL}}(p||q) = H(p,q) - H(p)$$Hay nói cách khác:$$ D_{\text{KL}}(p||q) = - \sum_{i=1}^{n} p_{i} \log_{b} \frac{q_{i}}{p_{i}} = \sum_{i=1}^{n} p_{i} \log_{b} \frac{p_{i}}{q_{i}}$$

Một số tính chất của Kullback–Leibler divergence như sau:

  • Kullback–Leibler divergence luôn luôn là một số không âm $ D_{\text{KL}}(p||q) \ge 0 $. Lý do bởi vì $\text{H} (p,q) \ge \text{H} (p)$ mà chúng ta đã đề cập phần trước. Dấu bằng xảy ra khi và chỉ khi $p_{i} = q_{i}$ với $\forall i$.

  • Cực tiểu hóa Kullback–Leibler divergence tương đương với cực tiểu hóa Cross Entropy.

  • Kullback–Leibler divergence không phải là một khoảng cách mêtric do nó không đối xứng. Hay nói cách khác $ D_{\text{KL}}(p||q) \ne D_{\text{KL}}(q||p)$, do đó trong các bài toán thì cần suy xét chọn lựa phù hợp.

Kullback–Leibler divergence một độ đo có nhiều ứng dụng rộng rãi trong máy học thống kê (đôi khi được gọi là độ đo information gain), một số thuật toán Data Visualization được sử dụng nhiều như t-SNE (t-distributed stochastic neighbor embedding).

4. Phần kết

Trong bài viết này ThetaLog giới thiệu với các bạn về những nội dung:

  • Định lượng thông tin của lý thuyết thông tin: xây dựng độ đo thông tin dựa trên xác suất của một sự kiện.
  • Độ đo Entropy: đo lượng thông tin trung bình của một biến ngẫu nhiên, Entropy càng cao thì phân bố càng đều càng bất định (khó dự đoán).
  • Độ đo Cross Entropy: đo lượng thông tin trung bình khi dùng mã hóa thông tin của một phân bố cho phân bố đích, lượng thông tin trung bình này luôn cao hơn Entropy.
  • Độ đo Kullback–Leibler divergence: là hiệu của Cross Entropy trừ cho Entropy, đo độ tương tự giữa phân bố được đo và phân bố kỳ vọng, là lượng thông tin trung bình thêm vào khi sử dụng mã hóa thông tin của phân bố $q$ cho phân bố $p$.

Trong lý thuyết thông tin thì cơ số $b=2$ được sử dụng để định lượng thông tin trên đơn vị bits, tuy nhiên trong các mô hình học máy thống kê thì cơ số thường được chọn là $e$ (đơn vị nats) của logarit tự nhiên.

We know the past but cannot control it. We control the future but cannot know it.
— Claude E. Shannon

Tham khảo

  1. David J. C. MacKay. Information Theory, Inference and Learning Algorithms. Cambridge University Press. 2003. (http://www.inference.org.uk/itprnn/book.html)

  2. C. E. Shannon. A Mathematical Theory of Communication. The Bell System Technical Journal. July, October, 1948. (http://math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf)

  3. Rob DiPietro. A Friendly Introduction to Cross-Entropy Loss. Version 0.1 – May 2, 2016. (https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/)

  4. Wikipedia contributors. “Information theory.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 25 Jun. 2018. Web. 27 Jul. 2018.

  5. Wikipedia contributors. “A Mathematical Theory of Communication.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 24 Jul. 2018. Web. 28 Jul. 2018.

  6. Wikipedia contributors. “Self-information.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 31 Jul. 2018. Web. 5 Aug. 2018.

  7. Wikipedia contributors. “History of entropy.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 31 Jul. 2018. Web. 6 Aug. 2018.