FastICA Independent Component Analysis Phân tích thành phần độc lập

Đăng trên bởi Lê Quang Tiến 26 phút trôi qua :D
Nội dung bài viết

Independent Component Analysis (phân tích thành phần độc lập) là một phương pháp thống kê được xây dựng để tách rời tín hiệu nhiều chiều thành các thành phần tín hiệu độc lập ẩn sâu bên dưới dữ liệu. Kỹ thuật này đòi hỏi phải đặt ra giả thuyết tồn tại các nguồn tín hiệu bên dưới nongaussianity và độc lập thống kê từng đôi một. Thuật toán ICA có nhiều ứng dụng rộng rãi trong nhiều bài toán khác nhau như xử lý tín hiệu, kinh tế học, sinh tin học,…

Xung quanh chúng ta, tồn tại rất nhiều nguồn tín hiệu phát ra một cách độc lập, độc lập ở đây có thể hiểu một cách nôm na là chẳng liên quan ảnh hưởng gì đến nhau trong việc tạo ra tín hiệu, tuy nhiên việc thu thập dữ liệu đôi lúc lại hòa trộn các nguồn vào nhau. Liệu có một giải pháp nào đó mà chúng ta có thể khôi phục dữ liệu về dạng nguyên bản, không trộn lẫn vào nhau hay không?

Dữ liệu nhiều chiều thường có thể được xem như những con số đo lường được sinh ra một cách gián tiếp từ những nguồn bên dưới không quan sát được. Một số ví dụ cụ thể:

  • Trong tâm lý học, những bài kiểm tra thường đưa ra nhiều câu hỏi thực tế để đo những yếu tố không quan sát được ở bên dưới, chẳng hạn đo lường về: sự tự tin, lòng dũng cảm,…

  • Điện não đồ (EEG - Electroencephalography): là một phương pháp ghi lại xung điện từ các nơ ron trong não, ICA được sử dụng để tách các tín hiệu này thành các tín hiệu thành phần độc lập bên dưới, nhằm khử nhiễu, lựa chọn những đặc trưng phù hợp.

  • Trong sinh tin học, người ta làm thí nghiệm với mỗi tế bào để thu về một mức biểu hiện nào đó với gien, dữ liệu thu thập được lưu thành một ma trận biểu hiện để phục vụ phân tích. Liệu có những nhân tố độc lập nào ẩn sâu bên dưới chi phối toàn bộ quá trình tạo nên những biểu hiện này?

ICA (Independent Component Analysis) và PCA (Principal Component Analysis) là hai phương pháp có mô hình tương tự nhau, chỉ khác nhau cách đặt ra giả thuyết, dẫn đến cách giải quyết bài toán khác nhau. ICA giả thuyết rằng tồn tại một mô hình mà dữ liệu có thể biểu diễn từ những biến ngẫu nhiên bên dưới độc lập thống kê, mặt khác PCA giả thuyết rằng tồn tại một mô hình mà dữ liệu có thể biểu diễn từ những biến ngẫu nhiên bên dưới không tương quan.

ICA là một công cụ đắc lực để xây dựng các đặc trưng phù hợp và mạnh mẽ cho nhiều bài toán khoa học dữ liệu.

1. Một bài toán ví dụ minh họa

Trong một căn phòng nọ, gồm $3$ người nói chuyện độc lập với nhau, căn phòng được một “thám tử dữ liệu” gắn $3$ chiếc máy ghi âm ($X_1$, $X_2$ và $X_3$) ở những vị trí khác nhau.

Mỗi thời gian $t$, mỗi chiếc máy ghi lại được tín hiệu âm thanh bị trộn lẫn bởi giọng nói của cả ba người. Vì mỗi chiếc máy ghi âm đặt ở những vị trí khác nhau trong căn phòng, nên âm thanh thu được mỗi chiếc máy khác nhau, to hay nhỏ phụ thuộc vào khoảng cách chiếc máy ghi âm đặt gần hay xa.

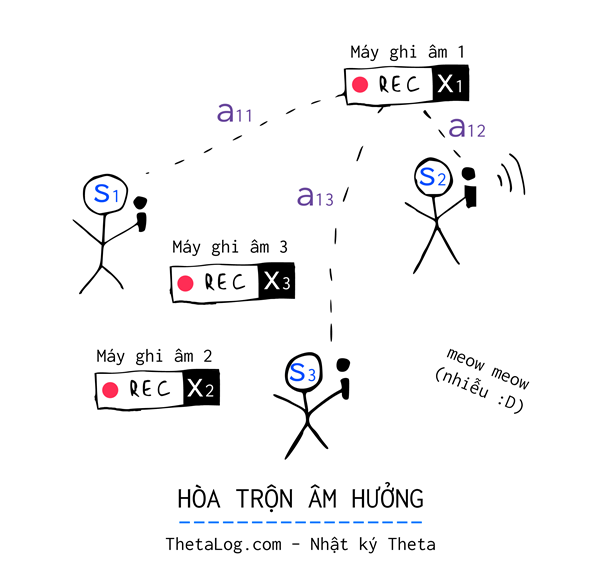
Gần xa, to nhỏ… nghĩ đi nghĩ lại có thể đặt một trọng số $a$ nào đấy thể hiện được sự phụ thuộc này. Như vậy chúng ta có thể tạm đặt $a_{ij}$ là trọng số của máy ghi âm $i$ thu được từ nguồn $j$, chẳng hạn:

$$ X_1 = a_{11} S_1 + a_{12} S_2 + a_{13} S_3$$

Hừm, các nguồn là độc lập, ông $S_1$ đang hát vu vơ “mây và tóc em bay trong chiều gió lộng…”, ông $S_2$ thì đang trả lời điện thoại, ông $S_3$ thì ngồi thẫn thờ đọc thơ… Ba âm thanh chẳng liên quan gì nhau hòa trộn lẫn lộn vào nhau được mỗi chiếc máy ghi âm ghi lại.

Dịch vụ theo dõi “bốn chấm không 4.0” khách hàng lại yêu cầu cần có cả bản thô và bản đã được xử lí để nghe rõ giọng từng người… phải làm sao bây giờ?

2. ICA Phân tích thành phần độc lập

2.1 Mô hình ICA

Giả sử chúng ta thu được $p$ biến ngẫu nhiên quan sát được $X_1, X_2,… X_p$ và giả định rằng mỗi biến ngẫu nhiên quan sát được $X_i$ có thể thể biểu diễn bởi $p$ biến ngẫu nhiên độc lập thống kê không quan sát được $S_1, S_2,… S_p$ phụ thuộc vào trọng số $a_{i1}, a_{i2},… a_{ip}$, chúng ta có thể viết lại mô hình ICA như sau:

$$ \begin{array}{*{20}{c}} X_1 & = & a_{11} S_1 + a_{12} S_2 + … + a_{1p} S_p \\ X_2 & = & a_{21} S_1 + a_{22} S_2 + … + a_{2p} S_p \\ \vdots & & \vdots \\ X_p & = & a_{p1} S_1 + a_{p2} S_2 + … + a_{pp} S_p \end{array} $$

Viết lại dạng ma trận:

$$ \underbrace {\color{#ff2d55} X}_{(p \times 1)} = \underbrace {\mathbf{A}}_{(p \times p)} \underbrace {\color{#ff2d55} S}_{(p \times 1)} $$

Vector ngẫu nhiên $X$ có thể biểu diễn bởi tích ma trận $A$ với vector ngẫu nhiên $S$.

Mô hình ở trên với $S_1, S_2,… S_p$ độc lập thống kê là mô hình ICA, điều chúng ta cần tìm là ma trận $A$ (ma trận trộn), tuy nhiên nếu không giả định gì thêm, việc tìm ra mô hình trên là bất khả thi, bởi vì có quá nhiều tham số cần ước lượng!

2.2 Một vài vấn đề nhập nhằng trong mô hình

2.2.1 Không thể xác định phương sai của các thành phần độc lập

Thật vậy, lý do đơn giản nếu chúng ta có một đại lượng vô hướng $c$, việc nhân và chia cho $c$ trong mô hình ICA tạo thành một mô hình mới mà vẫn thỏa các giả thuyết ban đầu:

$$ \begin{array}{*{20}{l}} {\color{#ff2d55} X} & = & \mathbf{A} {\color{#ff2d55} S} \\ & = & (c \mathbf{A}) {\color{#ff2d55} (S/c) } \end{array}$$

Lưu ý rằng vector ngẫu nhiên $(S/c)$ trong trường hợp này vẫn độc lập thống kê từng thành phần.

Do đó có vô số lời giải có khả năng xảy ra. Với không gian lời giải như vậy, việc tìm ra một lời giải hợp lí là vô cùng khó khăn, vì thế chúng ta cần đặt thêm một số giả định để giải bài toán đặt ra. Giả định rằng $\mathbb{E}( S_i^2) = 1$.

Tuy nhiên vấn đề nhập nhằng trên vẫn là một vấn đề đau đầu, bởi vì nếu $c = -1$ chúng ta sẽ thu về một mô hình mà $S_i$ bị đảo chiều dẫu $\mathbb{E}( S_i^2) = 1$ không đổi.

May mắn thay, trong các trường hợp ứng dụng thực tế, nó không ảnh hưởng gì nhiều bởi vì chuyên gia có thể điều chỉnh kết quả cuối cùng dựa trên tri thức am hiểu về loại dữ liệu mà mình đang xử lý!

2.2.2 Mô hình trực giao, phép quay trực giao, không thể xác định thứ tự thành phần độc lập

Nếu như bạn đã quen với các mô hình Principal component analysis hay Factor Analysis thì có một khái niệm khá thú vị trong các mô hình này là phép quay varimax rotation (và quartimax rotation) để diễn giải các thành phần bên dưới, sỡ dĩ làm được điều này là vì có một điều thú vị trong mô hình trên.

Gọi $R$ là một ma trận $(p \times p)$ trực giao (orthogonal matrix), ta có $R^{\intercal} R = R R^{\intercal} = I$ với $I$ là ma trận đơn vị.

Thật thú vị:

$$ \begin{array}{*{20}{l}} {\color{#ff2d55} X} & = & \mathbf{A} {\color{#ff2d55} S} \\ & = & \mathbf{A} I {\color{#ff2d55} S} \\ & = & (\mathbf{A} R^{\intercal}) {\color{#ff2d55} (RS)} \\ & = & \mathbf{A}^{*} {\color{#ff2d55} S^{*}} \end{array}$$

Lúc này chúng ta có $S^{*} = RS$ là một vector ngẫu nhiên mới vẫn thỏa những giả định ban đầu. Thật nhập nhằng!

3. Thế nào là độc lập thống kê?

Như đã định nghĩa nôm na ở phần trước, độc lập thống kê hiểu đơn giản là không liên quan gì nhau.

Hai sự kiện bất kì, sự kiện này diễn ra cũng chẳng ảnh hưởng gì sự kiện còn lại. Việc một biến cố xảy ra cũng không ảnh hưởng tăng giảm khả năng xảy ra biến cố còn lại.

Khái niệm của độc lập thống kê được mở rộng để phù hợp với tập của nhiều biến cố hay nói cách khác biến ngẫu nhiên, trong trường hợp này thì hai biến ngẫu nhiên gọi là độc lập với nhau khi từng biến cố của chúng độc lập từng đôi một. Với hai biến ngẫu nhiên bất kỳ $v_1$, $v_2$, hai biến ngẫu nhiên độc lập khi hàm mật độ xác suất (hoặc hàm khối xác suất) phân bố hợp của chúng có thể biểu diễn:

$$p(v_1, v_2) = p(v_1) p(v_2)$$

Một trong những dạng yếu của độc lập thống kê là không tương quan. Hai biến ngẫu nhiên $v_1$ và $v_2$ được gọi là không tương quan, nếu như:

$$\mathbb{E}(v_1 v_2) - \mathbb{E}(v_1)\mathbb{E}(v_2) = 0$$

Nếu như hai biến ngẫu nhiên là độc lập thì chúng không tương quan. Tuy nhiên điều ngược lại thì không đúng. Đây chỉ là điều kiện cần, không phải điều kiện đủ.

Từ khi độc lập thống kê suy ra không tương quan, nhiều phương pháp ICA được xây dựng sao có thể sinh ra ước lượng không tương quan cho các thành phần độc lập bên dưới dữ liệu. Việc này làm giảm số lượng tham số cần ước lượng cũng như đơn giản vấn đề bài toán.

4. Cơ sở lý luận ICA

4.1 Lập luận “nongaussianity thì độc lập”

Một cách trực cảm, chìa khóa dẫn đến lời giải của ICA đó chính là giả định các thành phần $S_i$ bên dưới dữ liệu nongaussianity (tức không gần giống với phân bố chuẩn).

Định lý giới hạn trung tâm (CLT - Central limit theorem) là một định lý cổ điển trong lý thuyết xác suất thống kê. Nó là chìa khóa cho ý tưởng của bài toán phân tích thành phần độc lập. Định lý giới hạn trung tâm phát biểu rằng phân bố tổng của tập các biến mẫu nhiên độc lập có phân bố khuynh hướng tiến về phân bố chuẩn với một số điều kiện.

Giả định rằng vector ngẫu nhiên $X$ được phân phối bởi các thành phần độc lập bên dưới dữ liệu:

$$ \color{#ff2d55} X \color{#37474f} = \mathbf{A} \color{#ff2d55}S$$

Nếu như chúng ta tìm được ma trận $\mathbf{A}$, việc ước lượng vector ngẫu nhiên $S$ tìm bởi mô hình:

$$ S = \mathbf{A}^{-1} X$$

Do đó, nếu chỉ cần ước lượng được duy nhất một thành phần độc lập, chúng ta có thể chỉ cần tìm một vector trọng số tổ hợp tuyến tính từ $X_i$.

Gọi $y = \mathbf{w}^{\intercal} X$ với $\mathbf{w}$ là vector trọng số $p \times 1$. Như vậy lúc này $y$ là một tổ hợp tuyến tính các thành phần từ $X$.

Tuy nhiên do $X = \mathbf{A} S$ nên ta có thể biểu diễn lại $y = \mathbf{w}^{\intercal} \mathbf{A} S$. Đặt $\mathbf{q}^{\intercal} = \mathbf{w}^{\intercal} \mathbf{A}$ ta có:

$$ y = \mathbf{w}^{\intercal} X = \mathbf{q}^{\intercal} S $$

Nếu như $\mathbf{w}$ là một hàng của $\mathbf{A}^{-1}$, tổ hợp tuyến tính $\mathbf{w}^{\intercal} X$ có thể chính là một trong các thành phần độc lập $S_i$. Trong trường hợp này, nếu điều trên xảy ra thì $\mathbf{q}$ sẽ là một vector mà chỉ có duy nhất một phần tử bằng $1$ còn tất cả còn lại là $0$ (như vậy $\mathbf{q}^{\intercal} S$ chính xác bằng một trong các thành phần $S_i$).

Câu hỏi đặt ra ngay bây giờ là: Làm cách nào mà chúng ta có thể sử dụng định lí giới hạn trung tâm để tìm $\mathbf{w}$ mà nó chính là một hàng của ma trận $\mathbf{A}^{-1}$?

Mẹo nằm ở đây, từ khi phân bố của tổng các biến ngẫu nhiên độc lập thì gaussian nhiều hơn từng thành phần độc lập, khi đó $y$ được biểu diễn $\mathbf{q}^{\intercal} S$ nên $y$ hay $\mathbf{w}^{\intercal} X$ thì gaussian nhiều hơn $S_i$ bất kì nhưng lại ít gaussian hơn khi nó thực sự chính bằng một thành phần độc lập $S_i$.

Do đó chúng ta có thể cực đại nongaussianity của $y$ hay $\mathbf{w}^{\intercal} X$ để thu về một thành phần độc lập.

4.2 Đo lường nongaussianity bằng Negentropy

Để đo lường nongaussianity trong mô hình ICA, có nhiều cách khác nhau (ví dụ như Kurtosis hay moment thứ 4, tuy nhiên kurtosis rất nhạy cảm với các điểm dị biệt), phương pháp ThetaLog chọn trình bày là Negentropy làm độ đo vì tính ổn định cao.

Negentropy là một độ đo thông tin dựa trên differential entropy để đo lường khoảng cách thông tin đến phân bố chuẩn cùng kỳ vọng và phương sai của phân bố gốc. Ý nghĩa của độ đo entropy trong lý thuyết thông tin bạn đọc có thể tham khảo thêm tại bài viết sau ThetaLog - Lý thuyết thông tin.

Differential entropy là độ đo entropy dành cho biến ngẫu nhiên liên tục $y$ với hàm mật độ xác suất $p(y)$:

$$H(y) = -\int p(y) \log p(y) \text{d}y$$

Negentropy là hiệu của hai Differential entropy của một biến ngẫu nhiên $y_{\text{gauss}}$ (cùng kỳ vọng và phương sai với $y$) cùng với $y$ được định nghĩa như sau:

$$J(y) = H(y_{\text{gauss}}) - H(y)$$

Trong lý thuyết thông tin (information theory), một trong những công trình cơ bản của (Cover and Thomas, 1991; Papoulis, 1991) chứng minh rằng biến ngẫu nhiên có phân bố chuẩn có entropy cao nhất trong số tất cả các biến ngẫu nhiên có cùng phương sai (a gaussian variable has the largest entropy among all random variables of equal variance), phần chứng minh sẽ không được trình bài ở đây, bạn đọc tự tìm hiểu thêm.

Do đó lúc này $J(y)$ là một hàm không âm, phản ánh mức độ gần phân bố gaussian của $y$.

Tuy nhiên việc tính toán $J(y)$ đòi hỏi ước lượng được hàm mật độ xác suất p.d.f của $y$, việc này thường phức tạp và khó khăn.

Thay vì tính toán trực tiếp như trên, Hyvärinen và Oja đề xuất một cách xấp xĩ:

$$J(y) \approx [ \mathbb{E} (G(y)) - \mathbb{E} ( G(y_{\text{gauss}}))]^2$$

Với $G$ là một hàm có nhiều sự lựa chọn:

$$ G_1(u) = \frac{1}{a_1} \log \cosh a_1 u \text{ với } 1 \le a_1 \le 2$$ $$ G_2(u) = -\exp \frac{-u^2}{2}$$

Với đạo hàm bậc $1$ đặt là $g(u)$ ta có:

$$g_1(u) = \tanh (a_1 u)$$ $$g_2(u) = u \exp \frac{-u^2}{2} $$

Và đạo hàm bậc $2$ đặt là $g’(u)$ ta có:

$$g’_1(u) = a_1 (1 - \tanh^2 (a_1 u))$$ $$g’_2(u) = (1-u^2) \exp \frac{-u^2}{2}$$

5. Tiền xử lý ICA

Trong phần này, chúng ta sẽ cùng thảo luận về một số bước tiền xử lý thống kê trước khi sử dụng phương pháp phân tích thành phần độc lập.

5.1 Chỉnh tâm (Centering)

Một trong những bước cơ bản nhất cần thiết trong bước tiền xử lý là chỉnh tâm của dữ liệu thu thập được bằng cách trừ cho vector kỳ vọng $m = \mathbb{E}(X)$ để tạo thành dữ liệu mới.

Bước tiền xử lý này giúp thuật toán ICA đơn giản hơn. Nó không đồng nghĩa rằng là kỳ vọng không thể ước lượng được, sau khi ước lượng xong ma trận $\mathbf{A}$, bạn hoàn toàn có thể ước lượng vector kỳ vọng của $S$ và chỉnh tâm $S$ bằng cách cộng thêm một lượng $\mathbf{A}^{-1} m$.

5.2 Tẩy dữ liệu (Whitening)

Một trong những bước tiền xử lý quan trọng của ICA là tẩy dữ liệu (whitening) sau khi chỉnh tâm.

Trong thống kê, Whitening transformation (hay Sphering transformation) là một phép biến đổi tuyến tính nhằm biến đổi một vector ngẫu nhiên với ma trận hiệp phương sai biết trước thành một tập biến ngẫu nhiên mới có ma trận hiệp phương sai là ma trận đơn vị. Hay nói cách khác phép biến đổi này biến đổi một tập biến ngẫu nhiên tương quan thành một tập biến ngẫu nhiên mới không tương quan và có phương sai là $1$.

Một cách hình thức, bài toán này tìm một cách biểu diễn vector ngẫu nhiên $\tilde X$ bởi tổ hợp tuyến tính từ $X$ từ ma trận $\mathbf{P}$ tức $\tilde X = \mathbf{P} X$ sao cho:

$$ \mathbb{E}(\tilde X \tilde X^{\intercal}) = I$$

Rất phương pháp được xây dựng để giải quyết bài toán này, bạn đọc quan tâm có thể tham khảo một số phương pháp sau:

  • ZCA-Mahalanobis whitening
  • Cholesky whitening
  • PCA whitening

Tính hữu ích của việc làm này là gì?

Quan sát kỹ ta thấy (đặt $\tilde {\mathbf{A}} = \mathbf{PA}$):

$$\tilde X = \mathbf{P}X = \mathbf{P} \mathbf{A} S = \tilde {\mathbf{A}} S$$

Ta có:

$$ \mathbb{E}(\tilde X \tilde X^{\intercal}) = I \tag{1}$$ $$ \mathbb{E}(\tilde X \tilde X^{\intercal}) = \mathbb{E}(\tilde {\mathbf{A}} S S^{\intercal} \tilde {\mathbf{A}}^{\intercal}) = \tilde {\mathbf{A}} \mathbb{E}(S S^{\intercal}) \tilde {\mathbf{A}}^{\intercal} = \tilde {\mathbf{A}} I \tilde {\mathbf{A}}^{\intercal} = \tilde {\mathbf{A}} \tilde {\mathbf{A}}^{\intercal} \tag{2}$$

Từ $(1)$ và $(2)$ ta có:

$$ \tilde {\mathbf{A}} \tilde {\mathbf{A}}^{\intercal} = I$$

Hay nói cách khác $\tilde {\mathbf{A}}$ là một ma trận trực giao (orthogonal matrix)!

Ở đây chúng ta thấy rằng công đoạn này rất hữu ích và đặc biệt quan trọng bởi vì nó làm giảm đi số lượng tham số cần phải ước lượng. Thay vì chúng ta phải ước lượng $p^2$ tham số, hay nói cách khác đó chính là số lượng tham số một ma trận vuông bình thường, tuy nhiên một ma trận trực giao thì chỉ có $p(p-1)/2$ bậc tự do hay nói cách khác chỉ có $p(p-1)/2$ tham số cần ước lượng! Do đó, công đoạn này đặc biệt giúp thuật toán ICA trở nên đơn giản và ổn định hơn.

6. FastICA

Trong phần này, chúng ta xem như dữ liệu đã được tiền xử lý ở phần trên.

6.1 FastICA cho duy nhất một thành phần độc lập

Với bài toán “tìm duy nhất một thành phần độc lập”, bài toán tương đương với việc chúng ta cần tìm vector trọng số $\mathbf{w}$ cực đại nongaussianity $y = \mathbf{w}^{\intercal} X$ hay nói cách khác chúng ta sẽ đi cực đại hàm $J(\mathbf{w}^{\intercal} X)$.

Tối ưu hàm $J(\mathbf{w}^{\intercal} X)$ với thỏa mãn điều kiện $\mathbb{E} ( (\mathbf{w}^{\intercal} X)^2) = ||\mathbf{w}||^2 = 1$ theo $w$ theo hàm Langrange, ta cần gradient của Lagrangian bằng $0$ hay nói cách khác:

$$ \mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \beta \mathbf{w} = 0 $$

(điều kiện của gradient này đã được tinh chỉnh, về mặt bản chất phải xuất hiện $\gamma = \mathbb{E} (G(\mathbf{w}^{\intercal} X)) - \mathbb{E}(G(y_{gauss}))$ đã được loại bỏ, lý do $\gamma$ có ảnh hưởng đến sự ổn định của thuật toán, hơn nữa với việc phân tích chúng ta thấy rằng loại bỏ $\gamma$ không ảnh hưởng đến kết quả mong muốn cuối cùng bởi vì $\mathbf{w}$ chúng ta sẽ thực hiện một bước chuẩn hóa bên dưới, bạn đọc quan tâm có thể đọc thêm [3] sách Independent Component Analysis )

Để giải phương trình trên chúng ta có thể sử dụng phương pháp Newton. Đặt về trái là $F$, ta có ma trận Jacobian tương ứng là:

$$JF(\mathbf{w}) = \mathbb{E} (XX^{\intercal} g’(\mathbf{w}^{\intercal} X) ) - \beta I$$

Từ khi dữ liệu của chúng ta đã được whitening, lúc này ta có $\mathbb{E}(XX^{\intercal} g’(\mathbf{w}^{\intercal}X)) \approx \mathbb{E} (XX^{\intercal}) \mathbb{E} (g’(\mathbf{w}^{\intercal}X))$ do đó $\mathbb{E}(XX^{\intercal} g’(\mathbf{w}^{\intercal}X)) \approx \mathbb{E}(g’(\mathbf{w}^{\intercal} X))I$. Ta có:

$$JF(\mathbf{w}) \approx [\mathbb{E}(g’(\mathbf{w}^{\intercal} X)) - \beta ] I$$

Lưu ý rằng $JF(\mathbf{w})$ hiện tại là một giá trị vô hướng, do đó thay vì lấy ma trận nghịch đảo của $JF(\mathbf{w})$ (ma trận đường chéo do nhân với $I$) chúng ta có thể chia thẳng cho đại lượng vô hướng này, ta có công thức cập nhật $\mathbf{w}^{+}$ theo vector trọng số mới của $\mathbf{w}$ được tính theo phương pháp Newton:

$$\mathbf{w}^{+} \leftarrow \mathbf{w} - [JF(w)]^{-1} F(w)$$

Tương đương:

$$\mathbf{w}^{+} \leftarrow \mathbf{w} - [\mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \beta \mathbf{w} ] / [\mathbb{E}(g’(\mathbf{w}^{\intercal} X)) - \beta ]$$

Nhân hai vế cho $\beta - \mathbb{E}(g’(\mathbf{w}^{\intercal} X))$ ta có:

$$ [\beta - \mathbb{E}(g’(\mathbf{w}^{\intercal} X))] \mathbf{w}^{+} \leftarrow [\beta - \mathbb{E}(g’(\mathbf{w}^{\intercal} X))] \mathbf{w} + [\mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \beta \mathbf{w} ] $$

Đơn giản hóa:

$$ [\beta - \mathbb{E}(g’(\mathbf{w}^{\intercal} X))] \mathbf{w}^{+} \leftarrow \mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \mathbb{E}(g’(\mathbf{w}^{\intercal} X)) \mathbf{w} $$

Hay nói cách khác:

$$ \psi \mathbf{w}^{+} \leftarrow \mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \mathbb{E}(g’(\mathbf{w}^{\intercal} X)) \mathbf{w} $$

Lưu ý hiện tại $\psi$ đóng vai trò giống như một hệ số tỷ lệ cho $\mathbf{w}^{+}$, tuy nhiên do điều kiện chúng ta mong muốn trọng số $||\mathbf{w}^{+}|| = 1$, hơn nữa phần nhập nhằng ban đầu nếu như $\mathbf{w}^{+}$ được chấp nhận thì $-\mathbf{w}^{+}$ cũng sẽ được chấp nhận, do đó ở đây chúng ta có thể hoàn toàn đơn giản thuật toán bằng cách cố định dấu $\mathbf{w}^{+}$ bằng cách bỏ $\psi$ và thêm một công đoạn chuẩn hóa $\mathbf{w}^{+}$ trong thuật toán.

Hay nói cách khác:

$$ \mathbf{w}^{+} \leftarrow \mathbb{E} (X g(\mathbf{w}^{\intercal}X)) - \mathbb{E}(g’(\mathbf{w}^{\intercal} X)) \mathbf{w} $$

$$ \mathbf{w}^{+} \leftarrow \mathbf{w}^{+} / ||\mathbf{w}^{+}||$$

Mã giả của thuật toán dưới cách nhìn mô hình toán học cho vector ngẫu nhiên $X$:

FUNCTION FastICA-One-Unit:
 $\mathbf{w} \leftarrow$ tạo ngẫu nhiên vector cột $p$ chiều
 Do {
  $\mathbf{w} \leftarrow \mathbb{E}(Xg(\mathbf{w}^{\intercal}X)) - \mathbb{E}(g'(\mathbf{w}^{\intercal}X))\mathbf{w}$
  $\mathbf{w} \leftarrow \mathbf{w} / ||\mathbf{w}||$
  } While (chưa hội tụ)
 RETURN $\mathbf{w}$

6.2 FastICA cho nhiều thành phần

Như đã nói ở phần việc, việc whitening dữ liệu là cực kì quan trọng, bởi vì giờ đây chúng ta có thể giả định là ma trận $\mathbf{A}$ là một ma trận trực giao. Do đó để tránh các vector trọng số hội tụ về cùng một điểm cực trị, chúng ta cần phải trực giao hóa tập vector $\mathbf{w}_{1} , \mathbf{w}_{2}, … \mathbf{w}_{p}$.

Gọi $\mathbf{W}$ là ma trận trọng số mà mỗi một hàng là $\mathbf{w}_{1}^{\intercal} , \mathbf{w}_{2}^{\intercal}, … \mathbf{w}_{p}^{\intercal}$, chúng ta có thể sử dụng thuật toán trực giao hóa đối xứng:

FUNCTION Symetric-Orthogonalization$(\mathbf{W})$:
 // Input: ma trận trọng số $\mathbf{W}$
 $\mathbf{W} \leftarrow (\mathbf{W} \mathbf{W}^{\intercal})^{-1/2} \mathbf{W}$
 RETURN $\mathbf{W}$

Lúc này chúng ta có thuật toán FastICA cho nhiều thành phần:

FUNCTION FastICA-Serveral-Units:
 $\mathbf{W} \leftarrow$ tạo ma trận ngẫu nhiên $p \times p$ với mỗi hàng là $\mathbf{w}_1, \mathbf{w}_2,... \mathbf{w}_p$
 Do {
  Foreach $\mathbf{w_i}$:
   $\mathbf{w}_i \leftarrow \mathbb{E}(Xg(\mathbf{w_i}^{\intercal}X)) - \mathbb{E}(g'(\mathbf{w_i}^{\intercal}X))\mathbf{w_i}$
  $\mathbf{W} \leftarrow $Symetric-Orthogonalizatio($\mathbf{W}$)
 } While (chưa hội tụ)
 RETURN $\mathbf{w}$

7. Cài đặt thuật toán

Mã giả thuật toán đã được trình bày như trên, tuy nhiên đó chỉ là những lập luận hình thức, thật thiếu sót nếu như chúng ta không thử cài đặt thuật toán từ những ý tưởng được xây dựng. Thuật toán được xây dựng tính toán vectorize nhằm tăng tốc độ tính toán.

Trong phần này ThetaLog sẽ cài đặt thuật toán dưới hai ngôn ngữ phổ biến là Python và R. Lưu ý là dữ liệu được tạo nhân tạo với Python, tuy nhiên bạn đọc có thể nạp dữ liệu sang R do mình đã lưu dữ liệu sang file .csv và lưu tại repo: https://github.com/quangtiencs/theta-notebook

7.1 Chuẩn bị dữ liệu thí nghiệm

Phần dữ liệu này mình sẽ tạo với Python.

Nạp một số thư viện, tinh chỉnh cần thiết:

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import scipy
from sklearn.decomposition import PCA
from matplotlib import style

style.use('bmh')
np.random.seed(0)

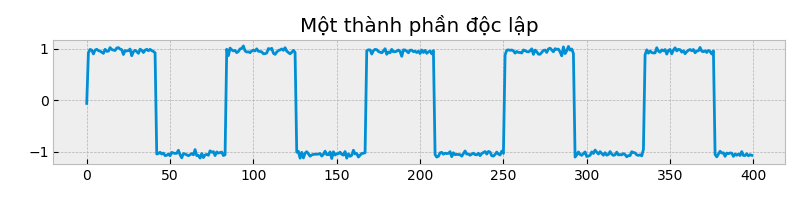
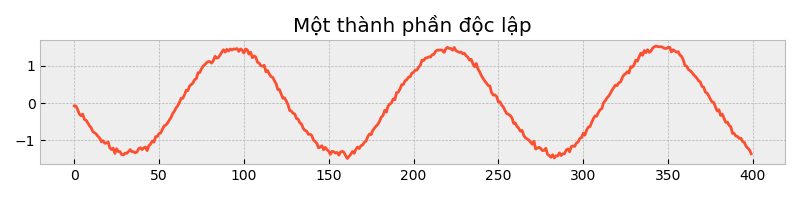
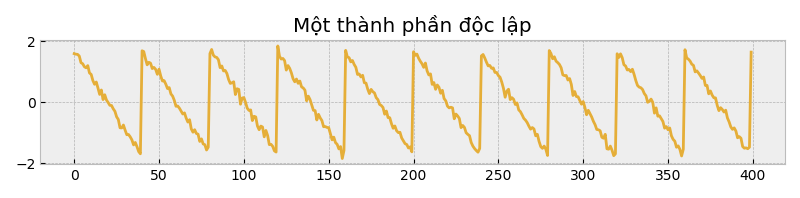
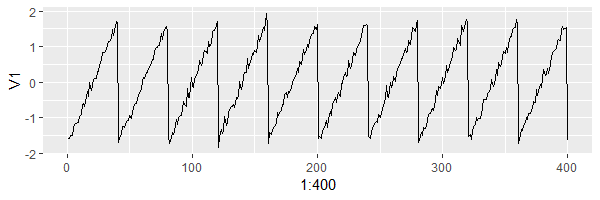
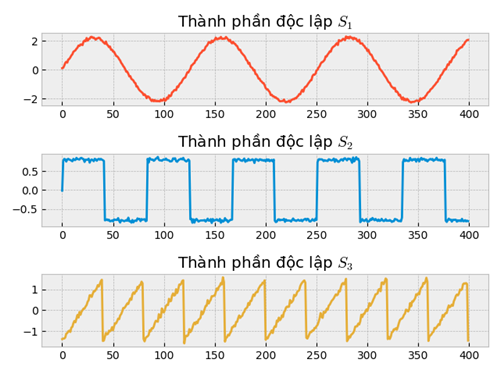
Tạo dữ liệu nguồn độc lập $S$ bên dưới:

n_samples = 400
time = np.linspace(0, 10, n_samples)

s1 = 2.2*np.sin(2 * time)
s2 = 0.8*np.sign(np.sin(3 * time))
s3 = 1.5*signal.sawtooth(2 * np.pi * time)

noise1 = 1.5*np.random.normal(loc=0.0, scale=0.04, size=n_samples)
noise2 = 0.7*np.random.normal(loc=0.0, scale=0.04, size=n_samples)
noise3 = 2.1*np.random.normal(loc=0.0, scale=0.04, size=n_samples)

S = np.c_[s1+noise1, s2+noise2, s3+noise3]

Visualize dữ liệu:

plt.figure()

fig = plt.subplot(3, 1, 1)
fig.set_title("Thành phần độc lập $S_1$")
plt.plot(S[:, 0], color="#fc4f30")

fig = plt.subplot(3, 1, 2)
fig.set_title("Thành phần độc lập $S_2$")
plt.plot(S[:, 1], color="#008fd5")

fig = plt.subplot(3, 1, 3)
fig.set_title("Thành phần độc lập $S_3$")
plt.plot(S[:, 2], color="#e5ae38")

plt.show()

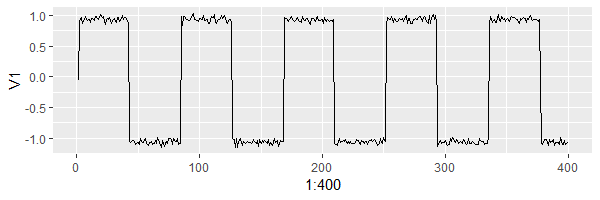
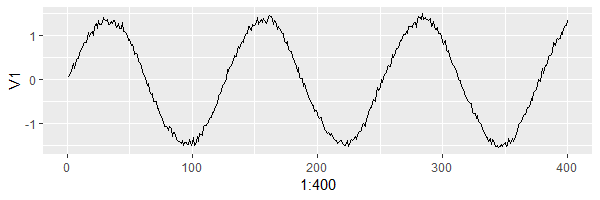
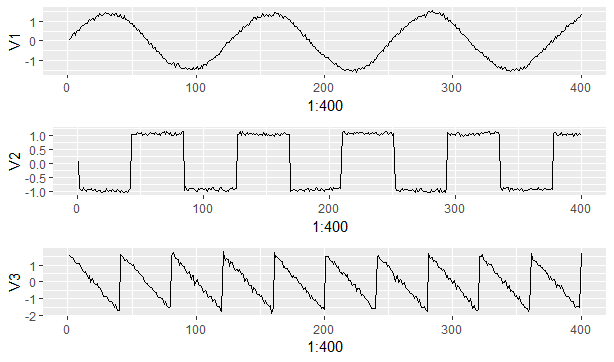
Chúng ta sẽ bắt tay vào việc trộn các thành phần này vào nhau bằng ma trận $\mathbf{A}$ một ma trận mà chúng ta không quan sát được, tập dữ liệu được xây dựng nhân tạo như sau:

# Ma trận bên dưới không quan sát được
A = np.array([[1, 1.2, 0.8], 
              [0.5, 2, 1.0], 
              [1.5, 1.0, 2.0]])
# Tạo dữ liệu
X = S @ A.T

Thử visualize ra nhé:

fig = plt.subplot(3, 1, 1)
fig.set_title("Dữ liệu thu thập được $X_1$")
plt.plot(X[:,0], color="#6d904f")

fig = plt.subplot(3, 1, 2)
fig.set_title("Dữ liệu thu thập được $X_2$")
plt.plot(X[:,1], color="#8b8b8b")

fig = plt.subplot(3, 1, 3)
fig.set_title("Dữ liệu thu thập được $X_3$")
plt.plot(X[:,2], color="#810f7c")

plt.show()

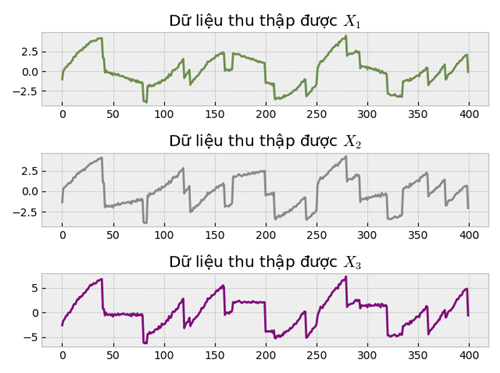
7.2 Tiền xử lý dữ liệu

def center_data(X):
    """Chỉnh tâm dữ liệu
    
    :param X: np.array - n dòng với p cột
    
    :return X_new: numpy.array - X sau khi được chỉnh tâm trừ cho trung bình
    """
    X_mean = X.mean(axis = 0)
    X_new = X - X_mean
    return X_new
    
def whiten_data(X):
    """Tẩy dữ liệu
    
    :param X: np.array - n dòng với p cột
    
    :return X_whiten: numpy.array - dữ liệu sau khi được whitening transformation
    """
    # sử dụng PCA để whitening
    pca = PCA(X.shape[1], whiten=True)
    X_whiten = pca.fit_transform(X)
    return X_whiten
Tiền xử lý dữ liệu: 
X = center_data(X)
X = whiten_data(X)
Mình chuẩn bị vài thứ để kết quả của chúng ta ra giống nhau 
set.seed(0)
Bạn đọc tải dữ liệu về, đọc dữ liệu lên bằng hàm: 
X <- as.matrix(read.csv("X.csv", header = F))
#' Chỉnh tâm dữ liệu
#'
#' @param X: matrix - n dòng với p cột
#'
#' @return X.new: matrix - X sau khi được chỉnh tâm trừ cho trung bình
#' 
centerData <- function(X){
  X.mean <- colMeans(X)
  X.new <- X - X.mean
  return(X.new)
}

#' Tẩy dữ liệu
#'
#' @param X: matrix - n dòng với p cột
#'
#' @return X.whiten: matrix - dữ liệu sau khi được whitening transformation
#' 
whitenData <- function(X){
  V <- t(X) %*% X / nrow(X)
  s <- La.svd(V)
  D <- diag(c(1/sqrt(s$d)))
  K <- D %*% t(s$u)
  
  X.whiten <- t(K %*% t(X))
  return(X.whiten)
}
Tiền xử lý dữ liệu: 
X <- centerData(X)
X <- whitenData(X)

7.3 Một số hàm hổ trợ (logcosh, exp)

def logcosh(y, alpha=1.0):
    """Hàm logcosh
    
    G(y) = 1/alpha * log(cosh(alpha y))
    g(y) = tanh(alpha * y)
    g'(y) = alpha ( 1 - tanh^2(alpha * y))
    
    :param y: np.array - p dòng với n cột
    
    :return gy: g(y) - shape (p, n)
    :return g_y: g'(y) - shape (p, n)
    """
    y = alpha * y
    gy = np.tanh(y)
    g_y = alpha * (1 - gy*gy)
    return gy, g_y


def exp(y):
    """Hàm exp
        
    G(y) = -exp[(-y^2) / 2] 
    g(y) = y exp[(-y^2) / 2] 
    g'(y) = (1-y^2) exp[(-y^2) / 2] 
    
    :param y: np.array - p dòng với n cột
    
    :return gy: g(y) - shape (p, n)
    :return g_y: g'(y) - shape (p, n)
    """
    exp = np.exp(-(y ** 2) / 2)
    gy = y * exp
    g_y = (1 - y ** 2) * exp
    return gy, g_y
#'
#' Hàm logcosh
#'
#' G(y) = 1/alpha * log(cosh(alpha y))
#' g(y) = tanh(alpha * y)
#' g'(y) = alpha ( 1 - tanh^2(alpha * y))
#' 
#' @param y: matrix - 1 dòng với n cột
#' @return result: list - g() & g'()
#' 
logcosh.func <- function(y, alpha=1){
  y <- alpha * y
  gy <- tanh(y)
  g2y = alpha * (1 - gy*gy)
  
  result <- list(gy=gy, g2y=g2y)
  return(result)
}

#'
#' Hàm exp (không đặt hàm exp vì trùng tên với R)
#'
#' G(y) = -exp[(-y^2) / 2] 
#' g(y) = y exp[(-y^2) / 2] 
#' g'(y) = (1-y^2) exp[(-y^2) / 2] 
#' 
#' @param y: matrix - 1 dòng với n cột
#' @return result: list - g() & g'()
#' 
exp.func <- function(y){
  exp.value <- exp(-(y ^ 2) / 2)
  gy <- y * exp.value
  g2y <- (1 - y ^ 2) * exp.value
  
  result <- list(gy=gy, g2y=g2y)
  return(result)
}

7.4 FastICA cho một thành phần độc lập

def fastica_oneunit(X, g_func=logcosh, tolerance=1e-5, max_iter=1000):
    """ FastICA cho một thành phần độc lập
    (tính toán vectorize)
    
    :param X: np.array - n dòng với p cột
    :param g_func: function - hàm trả về g & g'
    :param tolerance: float - dung sai cho phép
    :param max_iter: số vòng lặp tối đa
    
    :return w: np.array - shape (1, p)
    """
    # m: số lượng mẫu, p: số lượng chiều
    m = X.shape[0]
    p = X.shape[1]
    
    # tạo ngẫu nhiên vector w
    w = np.random.normal(size=(1, p))
    
    for i in range(max_iter):
        wtx = w @ X.T
        gwtx, g_wtx = g_func(wtx)
        
        w_new = gwtx @ X / float(m) - g_wtx.mean(axis=1) * w
        w_new = w_new / np.linalg.norm(w_new)
        
        epsilon = np.linalg.norm(w_new @ w.T - 1)
        
        w = w_new
        
        if epsilon < tolerance:
            break
    return w
Thử nghiệm với seed 12: 
np.random.seed(12)

# Chạy FastICA cho một thành phần
w = fastica_oneunit(X)

estimate_s = w @ X.T
estimate_s = estimate_s.T

#Vẽ nào
plt.figure(figsize=(8,2))

plt.title("Một thành phần độc lập")
plt.plot(estimate_s, color="#008fd5")
plt.show()

Thử nghiệm với seed 50 
np.random.seed(50)

# Chạy FastICA cho một thành phần
w = fastica_oneunit(X)

estimate_s = w @ X.T
estimate_s = estimate_s.T

#Vẽ nào
plt.figure(figsize=(8,2))

plt.title("Một thành phần độc lập")
plt.plot(estimate_s, color="#fc4f30")
plt.show()

Thử nghiệm với seed 51 
np.random.seed(51)

# Chạy FastICA cho một thành phần
w = fastica_oneunit(X)

estimate_s = w @ X.T
estimate_s = estimate_s.T

#Vẽ nào
plt.figure(figsize=(8,2))

plt.title("Một thành phần độc lập")
plt.plot(estimate_s, color="#e5ae38")
plt.show()

#'
#'FastICA cho một thành phần độc lập
#'(tính toán vectorize)
#'
#' @param X: matrix - n dòng với p cột
#' @param g.func: function - hàm trả về g & g'
#' @param tolerance: float - dung sai cho phép
#' @param max.iter: số vòng lặp tối đa
#'
#' @return w: matrix - shape (1, p)
#' 
fastICA.one.unit <- function(X, g.func=logcosh.func, tolerance=1e-5, max.iter=1000){
  m <- nrow(X)
  p <- ncol(X)
  
  w <- t(rnorm(p))
  
  for (i in 1:max.iter){
    wtx <- w %*% t(X)
    g.res <- g.func(wtx)
    gy <- g.res$gy
    g2y <- g.res$g2y
    
    w.new <- gy %*% X /m - rowMeans(g2y)*w
    w.new <- w.new / sqrt(sum(w.new^2))
    
    epsilon <- w.new %*% t(w)
    
    w <- w.new
    
    if (epsilon < tolerance) {
      break
    }
  }
  return(w)
}
Thử nghiệm với ggplot2 
library(ggplot2)
Thử với seed 12: 
set.seed(12)
w <- fastICA.one.unit(X)
estimate.s <- t(w %*% t(X))
ggplot(as.data.frame(estimate.s),aes(x=1:400,y = V1)) + geom_line()

Thử với seed 52: 
set.seed(52)
w <- fastICA.one.unit(X)
estimate.s <- t(w %*% t(X))
ggplot(as.data.frame(estimate.s),aes(x=1:400,y = V1)) + geom_line()

Thử với seed 28: 
set.seed(28)
w <- fastICA.one.unit(X)
estimate.s <- t(w %*% t(X))
ggplot(as.data.frame(estimate.s),aes(x=1:400,y = V1)) + geom_line()

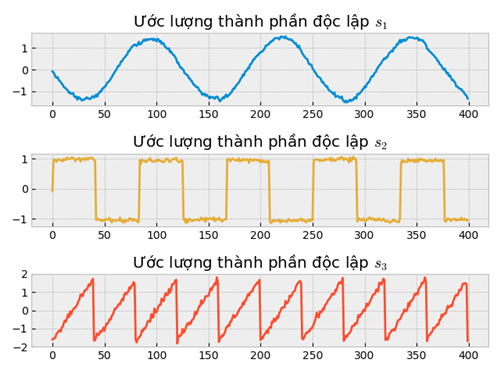
7.5 FastICA cho nhiều thành phần độc lập

def symetric_orthogonalization(W):
    """ Trực giao hóa đối xứng (xóa tương quan)
    
    :param W: np.array - p dòng với p cột
    :return W: np.array - p dòng với p cột
    """
    eigen_val, eigen_vec = np.linalg.eigh(np.dot(W, W.T))
    sqrt_wwt = (eigen_vec * (1. / np.sqrt(eigen_val))) @ eigen_vec.T
    return sqrt_wwt @ W


def fastica_symetric(X, g_func=logcosh, tolerance=1e-04, max_iter=1000):
    """ FastICA cho nhiều thành phần
    Parallel FastICA - dùng trực giao đối xứng 
    
    :param X: np.array - n dòng với p cột
    :param g_func: function - hàm trả về g & g'
    :param tolerance: float - dung sai cho phép
    :param max_iter: số vòng lặp tối đa
    
    :return W: np.array - shape (p, p) với mỗi hàng là w_i
    """
    m = float(X.shape[0])
    p = X.shape[1]
    
    # Tạo ngẫu nhiên
    W = np.asarray(np.random.normal(size=(p, p)))
    
    # Trực giao hóa
    W = symetric_orthogonalization(W)
    
    for i in range(max_iter):
        wxt = W @ X.T
        gwtx, g_wtx = g_func(wxt)
        
        W_new = (gwtx @ X) / float(m) - g_wtx.mean(axis=1).reshape(p, 1) * W
        W_new = symetric_orthogonalization(W_new)
        
        epsilon = float(np.max(np.abs(np.abs(np.diag(W_new @ W.T)) - 1)))
        
        W = W_new
        
        if epsilon < tolerance:
            break

    return W
Thử nghiệm thử nào 
W = fastica_symetric(X)

estimate_S = W @ X.T
estimate_S = estimate_S.T

# Vẽ nào
plt.figure()

fig = plt.subplot(3, 1, 1)
fig.set_title("Ước lượng thành phần độc lập $s_1$")
plt.plot(estimate_S[:,0], color="#008fd5")

fig = plt.subplot(3, 1, 2)
fig.set_title("Ước lượng thành phần độc lập $s_2$")
plt.plot(estimate_S[:,1], color="#e5ae38")

fig = plt.subplot(3, 1, 3)
fig.set_title("Ước lượng thành phần độc lập $s_3$")
plt.plot(estimate_S[:,2], color="#fc4f30")

plt.show()

#' Trực giao hóa đối xứng (xóa tương quan)
#' 
#' @param W: matrix - p dòng với p cột
#' @return W: matrix - p dòng với p cột
#'
symetric.Orthogonal <- function(W){
  sW <- La.svd(W)
  W <- sW$u %*% diag(1/sW$d) %*% t(sW$u) %*% W
  return(W)
}

#'
#'  FastICA cho nhiều thành phần
#'  Parallel FastICA - dùng trực giao đối xứng
#'  
#'  @param X: np.array - n dòng với p cột
#'  @param g_func: function - hàm trả về g & g'
#'  @param tolerance: float - dung sai cho phép
#'  @param max_iter: số vòng lặp tối đa
#'  
#'  @return W: np.array - shape (p, p) với mỗi hàng là w_i
fastICA.symetric <- function(X, g.func=logcosh.func, tolerance=1e-5, max.iter=1000){
  m <- nrow(X)
  p <- ncol(X)
  
  W <- matrix(rnorm(p*p), nrow=p)
  W <- symetric.Orthogonal(W)
  
  for (i in 1:max.iter){
    wtx <- W %*% t(X)
    g.res <- g.func(wtx)
    gy <- g.res$gy
    g2y <- g.res$g2y
    
    W.new <- gy %*% X /m - rowMeans(g2y)*W
    W.new <- symetric.Orthogonal(W.new)
    
    epsilon <- max(Mod(Mod(diag(W.new %*% t(W))) - 1))
    
    W <- W.new
    
    if (epsilon < tolerance){
      break
    }
  }
  return(W)
}
Thử nào 
 W <- fastICA.symetric(X)
data <- as.data.frame(t(W %*% t(X)))

g1 <- ggplot(as.data.frame(data),aes(x=1:400,y = V1)) + geom_line()
g2 <- ggplot(as.data.frame(data),aes(x=1:400,y = V2)) + geom_line()
g3 <- ggplot(as.data.frame(data),aes(x=1:400,y = V3)) + geom_line()

library(gridExtra)
grid.arrange(g1,g2, g3)

Tuyệt vời chưa nào!

8. Phần kết

ICA là một thuật toán rất hữu ích trong các bài toán khoa học dữ liệu khi tồn tại những nhân tố ẩn sâu bên dưới dữ liệu độc lập từng đôi một và nongaussianity. Một trong những thuật toán phổ biến thường được sử dụng là FastICA. Bạn đọc quan tâm có thể tìm hiểu thêm một số thuật toán khác, ví dụ: ProDenICA của Trevor Hastie, Rob Tibshirani cũng là một thuật toán ICA ổn định.

Chúc bạn có những giây phút vui vẻ bên thuật toán!

Ngày hoàn tất: 26-03-2019 (Lê Quang Tiến - quangtiencs)

Tham khảo

  1. Trevor Hastie, Robert Tibshirani, Jerome H. Friedman. The Elements of Statistical Learning. Springer Series in Statistics. https://web.stanford.edu/~hastie/ElemStatLearn/
  2. Aapo Hyvärinen và Erkki Oja. Independent Component Analysis: Algorithms and Applications. Neural Networks Research Centre. Helsinki University of Technology
  3. Aapo Hyvärinen, Juha Karhunen, Erkki Oja. Independent Component Analysis 1st Edition. Wiley-Interscience. ISBN-13: 978-0471405405. https://www.cs.helsinki.fi/u/ahyvarin/papers/bookfinal_ICA.pdf
  4. Hyvärinen, A. (1998b). New approximations of differential entropy for independent component analysis and projection pursuit. In Advances in Neural Information Processing Systems, volume 10, pages 273–279.MIT Press.
  5. Wikipedia contributors. “Whitening transformation.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 18 Jan. 2019. Web. 21 Mar. 2019.