Deferred-Acceptance Algorithm và bài toán hôn nhân bền vững
Nội dung bài viết
Deferred-Acceptance Algorithm (DAA - thuật toán chấp nhận trì hoãn) được đề xuất bởi David Gale và Lloyd Shapley nhằm giải quyết bài toán hôn nhân bền vững. Về sau những đóng góp lý thuyết về tính ổn định lời giải bài toán hôn nhân bền vững của Gale & Shapley và những nổ lực ứng dụng thực tiễn của Alvin Roth mang đến giải Nobel kinh tế học 2012.
Trở lại vào năm 1962, khi hai nhà toán kinh tế học David Gale và Lloyd Shapley đặt ra câu hỏi: “Liệu có thể thiết kế một quy trình tuyển sinh đại học, hoặc một quy trình tuyển dụng, sao cho các bên hợp tác tham gia trong một thị trường cung cầu hay không?”. Bài toán này như một mô hình lý thuyết trò chơi có hợp tác, các bên tham gia hợp tác để tối đa lợi ích toàn cục.
Hãy hình dung bài toán sau đây, việc tìm được việc làm mình yêu thích, việc tuyển được nhân viên tiềm năng là một bài toán cung cầu. Vấn đề nhân sự luôn là một bài toán hóc búa đối với nhà tuyển dụng. Hầu hết mọi công ty đều có chế độ thử việc, việc này nhằm giảm thiểu rủi ro tuyển người không phù hợp. Tuy nhiên hãy tưởng tượng một viễn cảnh sau đây xảy ra:
- Khoa vừa chấp nhận hợp đồng thử việc của công ty AlphaLog.
- Hai tuần sau, Khoa đột ngột nhận được cú điện thoại công ty khởi nghiệp BetaLog trước đây từng nộp hồ sơ mãi không hồi âm, đồng thời lời đề nghị phỏng vấn. Khoa vượt qua vòng phỏng vấn, BetaLog đưa ra hợp đồng thử việc mới mức phúc lợi cao hơn gấp $2$ lần so với AlphaLog, môi trường làm việc lại tốt hơn. Khoa quyết định hủy hợp đồng thử việc với AlphaLog và bắt đầu hành trình mới ở BetaLog.
- Mất đi một ứng cử viên, vài tháng tới lại có dự án cần hoàn thành gấp. AlphaLog quyết định đưa ra một hợp đồng với những ứng cử viên vẫn đang nằm trong danh sách chờ đợi chưa xét duyệt. Cuối cùng AlphaLog chọn được một bạn quyết định từ bỏ công việc ở GammaLog vì việc làm không phù hợp, hơn nữa đây là một ứng cử viên tìm năng. Mọi việc bắt đầu mất kiểm soát.
- Mọi việc vẫn chưa hẳn tồi tệ lắm đâu. Giả sử rằng bạn của Khoa là Học, hồ sơ của Học rất tốt, tuy nhiên vì một chút thiếu tự tin Học đang làm việc ở GammaLog. Nghe về câu chuyện của Khoa, Học biết mình đủ sức có thể ứng tuyển BetaLog. Học quyết định ứng tuyển vào BetaLog! Hồ sơ của Học thật tuyệt vời, đây là hồ sơ mà BetaLog tìm kiếm bấy lâu… vì BetaLog là một công ty khởi ngiệp không có nhiều thời gian suy xét, mà nguồn kinh phí lại có hạn, ai mà lại không thích tuyển người giỏi cơ chứ. BetaLog quyết định sa thải một nhân viên khác trong giai đoạn thử việc và tuyển Học.
Thị trường lao động rơi vào mất kiểm soát, dường như trong viễn cảnh trên, cả ứng cử viên và nhà tuyển dụng đều không mấy vui vẻ, mọi thứ cứ trong tình trạng hỗn loạn. Trong một môi trường kinh tế bất ổn định như thế, việc tạo ra giá trị cho xã hội sẽ mất nhiều thời gian hơn, đó là một sự lãng phí về kinh tế.
Trước những năm 1950, viễn cảnh trên không phải là ít, đặc biệt là trong môi trường tuyển dụng bác sĩ của các bệnh viện ở Mỹ. Mỗi bệnh viện đều mong muốn tuyển được bác sĩ giỏi:
- Do khó tìm người giỏi, để cạnh tranh các bệnh viện thường đưa ra hợp đồng ngay từ năm thứ 3 đại học của các bác sĩ giỏi.
- Vì biết rằng, mỗi bác sĩ giỏi sẽ có rất nhiều hợp đồng, nên các bệnh viện thường bắt buộc bác sĩ nhận được hợp đồng phải trả lời ngay trong vòng 12 tiếng, một hành động rất máy móc.
Một thị trường lao động như thế, ắt hẳn sẽ không hiệu quả, quá nhiều biện pháp tiêu cực đầy máy móc được áp dụng. Nó là nguồn cảm hứng của bài toán mà chúng ta muốn giải quyết!
1. Phát biểu bài toán hôn nhân bền vững
Để tiện cho việc phát biểu bài toán. Từ phần này trở về sau chúng ta sẽ phát biểu bài toán dưới dạng bài toán hôn nhân bền vững (Stable marriage problem).
Giả sử có $n$ cặp nam và nữ, một cách rất tự nhiên, hôn nhân thì phải phù hợp, mà phù hợp lại phải dựa trên những quan điểm cá nhân. Mỗi người lại có những tiêu chí đánh giá khác nhau, không thể đề ra hàng loạt tiêu chí và bắt người khác đánh giá được. Tuy nhiên quy cho cùng những tiêu chí đánh giá đó có thể đưa về một dạng thông tin hữu ích hơn, danh sách xếp hạng yêu thích!
Hôn nhân là một quan hệ hai ngôi giữa một nam và một nữ, bền vững là một khái niệm tương đối, trong bài toán này bền vững có nghĩa là yêu nhau mà khó lòng bỏ nhau được. Hãy xét ví dụ sau đây để hiểu rõ hơn:
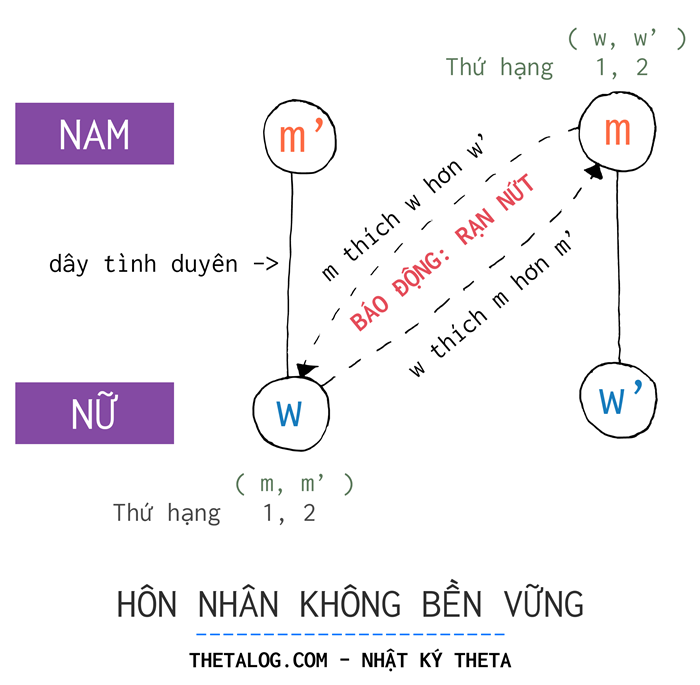
Hai cặp hôn nhân $\{ (m’, w), (m, w’) \}$ được gọi là không bền vững. Hiểu một cách nôm na hôn nhân không bền vững nghĩa là hai cặp hôn nhân có xu hướng rạn nứt bởi vì tồn tại một cặp không phải tình nhân nhưng họ yêu nhau hơn chính nhân tình của họ. Nói cách khác, $w$ kết hôn với $m’$ nhưng lại thích $m$ hơn $m’$, $m$ kết hôn với $w’$ nhưng lại thích $w$ hơn $w’$. Nếu như việc này xuất phát từ một phía thì chẳng sao cả, tất cả chỉ là trồng cây si mà thôi nhưng khi nó xuất phát từ hai phía hướng về nhau thì rõ ràng đây là hôn nhân không bền vững.
Giả định rằng hai bên cung cấp thông tin cho chúng ta, mỗi người tham gia sẽ có một danh sách xếp hạng yêu thích. Để tiện cho việc giải bài toán, chúng ta phát biểu bài toán dưới dạng:
Mong muốn xây dựng được một thuật toán:
Đầu vào - INPUT:
- Tập $n$ bạn nam $M = \{m_{1}, m_{2},… m_{n} \}$
- Tập $n$ bạn nữ $W = \{w_{1}, w_{2},… w_{n} \}$
- Danh sách xếp hạng yêu thích của của mỗi người được ký hiệu $\mathtt{PreferenceList}_{a}$, ví dụ xếp hạng yêu thích của bạn nam thứ nhất $\mathtt{PreferenceList}_{m_{1}} = (w_{12}, w_{28},…w_{7})$
- Gọi $P_{w_{i}}(m_{j})$ là thứ hạng mà bạn nữ thứ $i$ đánh giá bạn nam thứ $j$ trong danh sách xếp hạng yêu thích.
- Gọi $P_{m_{i}}(w_{j})$ là thứ hạng mà bạn nam thứ $i$ đánh giá bạn nữ thứ $j$ trong danh sách xếp hạng yêu thích.
- Lưu ý: thứ hạng càng thấp thì người đó càng được thích hơn, ví dụ $\mathtt{PreferenceList}_{m_{1}} = (w_{12}, w_{28},…w_{7})$, ta có $P_{m_{1}}(w_{12}) = 1 $ và $P_{m_{1}}(w_{28}) =2$ do đó $P_{m_{1}}(w_{12}) < P_{m_{1}}(w_{28})$ nghĩa là $m_{1}$ thích $w_{12}$ hơn $w_{28}$.
Đầu ra - OUTPUT:
- Hôn nhân bền vững $S \subseteq M \times W$, $S$ là một quan hệ hai ngôi của tập những bạn nam $M$ vào tập những bạn nữ $W$ vì thế $S$ là tập con của tích Descartes $ M \times W = \{(m,w) | m \in M \text{ và } w \in W \}$.
$S$ được gọi là ghép cặp bền vững khi và chỉ khi
- Tất cả đều kết hôn.
- Không tồn tại trường hợp hôn nhân có khả năng rạn nứt, với mọi cặp đôi đã kết hôn, không tồn tại hai cặp hôn nhân bất kì, mà bạn nam ở cặp thứ nhất thích bạn nữ ở cặp thứ hai hơn người yêu mình đồng thời bạn nữ ở cặp thứ hai thích bạn nam thứ nhất hơn người yêu của mình.
Một cách hình thức cho hai phát biểu trên:
$$ |S| =n \\ \forall m \in M, \exists w \in W, (m,w) \in S \\ \forall w \in W, \exists m \in M, (m,w) \in S \\ \neg \exists_{(m, w) \notin S} \left( (m, w’) \in S \land (m’, w) \in S \land \left( P_{m}(w) < P_{m}(w’) \right) \land \left( P_{w}(m) < P_{w}(m’) \right) \right) $$
Nhìn có vẻ dài dòng nhưng nó đảm bảo chúng ta cùng hiểu một cách phát biểu như nhau.
2. Thuật toán chấp nhận trì hoãn (Gale-Shapley Algorithm)
Thuật toán chấp nhận trì hoãn (Gale-Shapley Algorithm) được xây dựng trên ý tưởng
- Các bạn nữ tiếp tục trì hoãn câu trả lời mình sẽ kết hôn với ai, hẹn hò đến khi tìm được người tâm đầu ý hợp.
- Các bạn nam mãi đi tìm kiếm mảnh ghép cuộc đời của mình, dù thất bại (tỏ tình, bị chia tay) vẫn đứng lên làm lại từ đầu, khi đã yêu ai sẽ yêu thật lòng, không bao giờ bắt cá hai tay khi đang yêu ai đó.
Thuật toán chấp nhận trì hoãn có thể được diễn giải như sau:
Tại thời điểm khởi tạo, tất cả đều chưa hẹn hò.
Trong mỗi lượt, các bạn nam là người chủ động tỏ tình. Giả sử một bạn nam khi tỏ tình, ắt hẳn bạn ấy sẽ chọn ngay người mà mình yêu quý nhất mà mình có trong danh sách mà chưa bị từ chối hoặc chia tay. Khi nhận được lời tỏ tình, các bạn nữ độc thân chỉ chấp nhận mối quan hệ hẹn hò. Nếu có một bạn nam khác tỏ tình với một bạn nữ đang hẹn hò, có hai trường hợp có thể xảy ra, nếu bạn nữ thích giữ mối quan hệ hiện tại thì bạn nam sẽ đau lòng một đi không trở lại và không bao giờ quay lại tỏ tình nữa, nếu bạn nữ thích mối quan hệ mới hơn thì hai người sẽ hẹn hò, bạn trai cũ trở về trạng thái độc thân đi tìm mảnh ghép mới.
Lặp đi lặp lại quá trình trên mãi đến khi không còn bạn nam nào độc thân mà chưa tỏ tình với tất cả cô gái.
Mã giả thuật toán chấp nhận trì hoãn (Gale-Shapley Algorithm):
Khởi tạo trạng thái ban đầu $\forall w \in W$ và $\forall m \in M$ độc thân
While $\exists m$ độc thân chưa tỏ tình hết danh sách :
$w \leftarrow$ bạn nữ xếp hạng cao nhất danh sách yêu thích mà $m$ chưa tỏ tình
If $w$ đang độc thân:
Thêm $(m, w)$ vào $S$
Else lúc này $w$ đang hẹn hò cùng $m'$:
If $w$ thích $m$ hơn $m'$ hay $P_{w}(m) < P_{w}(m')$:
$m'$ bị chia tay trở về độc thân, xóa $(m', w)$ ra khỏi $S$
Thêm (m, w) vào $S$
Else $w$ thích $m'$ hơn $m$:
$m$ tiếp tục độc thân
Endif
Endif
Endwhile
RETURN $S$
Thuật toán dẫn đến giải Nobel kinh tế học 2012 chỉ vỏn vẹn vậy thôi sao? Sâu trong sự đơn giản ấy lại ẩn chứa nhiều điều tinh tế…
3. Phân tích thuật toán
Thiết kế thuật toán để giải quyết bài toán hôn nhân bền vững có khó lắm không? Lấy người mình yêu và không bỏ được… nghe thì rất dể, nhưng nếu bắt tay vào thiết kế thuật toán… phân tích tính đúng đắn và phân tích độ phức tạp… bạn sẽ thấy bài toán này thuộc dạng “không phải dạng vừa đâu”…
Vì sao vậy? Thiết kế một thuật toán hôn nhân bền vững nghĩa là nó phải tìm được $S \subseteq M \times W$ thỏa các điều kiện trên. Lưu ý là $M \times N$ có số phần tử rất lớn tận $n^2$… mà bài toán chúng ta cần làm là lấy ra tổ hợp các phần tử từ tập hợp $M \times N$ nghĩa là số cách chọn của $S$ rất lớn, thuật toán đưa ra lời giải cần phải có một chiến thuật đúng đắn trong không gian tìm kiếm rộng lớn để thỏa mãn ràng buộc.
Trước Gale-Shapley, rất nhiều nghiên cứu giải bài toán này. Tiêu biểu là thuật toán của bác Philip Hall, tiếc thay thuật toán chỉ đảm bảo rằng tập trả về là một tập ghép hoàn hảo (tất cả đều kết hôn) tuy nhiên lại không đảm bảo hôn nhân bền vững.
Gale-Shapley đưa ra một thuật toán khá đơn giản nhưng rất tinh tế, về sau rất nhiều biến thể được xây dựng dựa trên thuật toán gốc được ứng dụng vào các bài toán thực tiễn trong cuộc sống!
3.1 Tính đúng đắn
Thật vậy, nếu $w$ bị tỏ tình khi mình đang hẹn hò thì $w$ sẽ tìm được bạn nam mà mình thích hơn, hoặc không thích thì từ chối. Một khi $w$ đã hẹn hò cùng ai, mọi quyền quyết định phụ thuộc vào $w$, $w$ là người duy nhất có quyền chia tay - hẹn hò với người mới.
Thật vậy, nếu bạn nam bị chia tay, bạn ấy bắt buộc phải đi tìm mảnh ghép mới, mà chắc chắn rằng mảnh ghép này thứ hạng yêu thích sẽ thấp hơn (dựa trên danh sách yêu thích).
| Định lý 1: Ghép cặp hoàn hảo (Perfect Matching) |
|---|
| Kết quả của thuật toán chấp nhận trì hoãn là một tập ghép cặp hoàn hảo, tất cả đều kết hôn: $$ |S| =n \\\ \forall m \in M, \exists w \in W, (m,w) \in S \\\ \forall w \in W, \exists m \in M, (m,w) \in S $$ |
Chứng minh: Chứng minh phản chứng bằng nguyên lý chuồng bồ câu (nguyên lý ngăn kéo Dirichlet).
- Định lý nhỏ 1.1: Nếu tồn tại $m$ đang độc thân tại một thời điểm nào đó thì chắc chắn có ít nhất một bạn nữ mà $m$ chưa bao giờ tỏ tình.
Chứng minh Định lý nhỏ 1.1: Giả sử điều ngược lại, tại một thời điểm nào đó tồn tại $m$ đang độc thân mà đã tỏ tình với tất cả bạn nữ $w \in W$. Quan sát 1 cho chúng ta thấy rằng trong trường hợp giả sử này tất cả $w$ đều đang hẹn hò. Vì sao vậy? Để xảy ra điều này, đơn giản là $m$ bị từ chối tỏ tình hoặc bị chia tay với tất cả $n$ bạn nữ, mà trường hợp từ chối hay chia tay thì trạng thái $w$ vẫn đứng yên là hẹn hò. Tuy nhiên từ khi hẹn hò là một cặp $1$ nam và $1$ nữ, có $n$ bạn nữ hẹn hò tuy nhiên lại có ít hơn $n$ bạn nam (bởi vì $m$ đang độc thân), theo nguyên lý chuồng bồ câu, chúng ta không thể làm điều này. Từ đó suy ra điều phải chứng minh.
- Định lý nhỏ 1.2: Tập ghép cặp trả về là một tập ghép cặp hoàn hảo.
Chứng minh Định lý nhỏ 1.2: Giả sử thuật toán dừng mà vẫn tồn tại một bạn nam chưa kết hôn. Theo mã giả, thuật toán chỉ dừng khi $m$ đã tỏ tình với tất cả bạn nữ $w$. Tuy nhiên ở định lý nhỏ 1.1 chúng ta thấy rằng: “không thể tồn tại một $m$ đang độc thân mà đã tỏ tình với tất cả bạn nữ $w$”. Hay nói cách khác, giả sử trên không thể xảy ra. Từ đó suy ra điều phải chứng minh.
Vậy kết quả của thuật toán chấp nhận trì hoãn là một tập ghép cặp hoàn hảo.
| Định lý 2: Ghép cặp bền vững (Stable Matching) |
|---|
| Kết quả của thuật toán chấp nhận trì hoãn là một tập ghép cặp bền vững, không tồn tại hai cặp có xu hướng rạn nứt: $$ \neg \exists_{(m, w) \notin S} \left( (m, w') \in S \land (m', w) \in S \land \left( P_{m}(w) < P_{m}(w') \right) \land \left( P_{w}(m) < P_{w}(m') \right) \right)$$ |
Chứng minh: Giả định rằng $S$ không phải là tập ghép cặp bền vững.
Nghĩa là $\exists (m, w) \notin S$ mà $m$ và $w$ yêu nhau hơn nhân tình của họ, vì thuật toán trả về một tập ghép cặp hoàn hảo:
- Gọi $m’$ là kết quả hôn nhân của $w$ tìm bởi thuật toán, nói cách khác $(m’,w) \in S$
- Gọi $w’$ là kết quả hôn nhân của $m$ tìm bởi thuật toán, nói cách khác $(m,w’) \in S$
- Hôn nhân $ \{ (m’,w) , (m,w’) \}$ có xu hướng rạn nứt bởi $(m,w)$ hay nói cách khác $P_{m}(w) < P_{m}(w’)$ và $P_{m}(m) < P_{w}(m’)$ đồng loạt xảy ra.
Trong lúc chạy thuật toán để sinh ra $S$, nếu quan sát bạn sẽ thấy rằng lần tỏ tình cuối cùng của $m$ chính là $w’$, khi đang hẹn hò thì $m$ không bao giờ bắt cá hai tay, $m$ chỉ tiếp tục tìm kiếm mảnh ghép mới khi bị chia tay.
Bây giờ chúng ta đặt ra câu hỏi: Liệu $m$ đã tỏ tình với $w$ tại một giai đoạn nào đó trong lúc thực thi thuật toán không?
- Nếu không, nghĩa là $m$ thích $w’$ hơn $w$, một cách hình thức $P_{m}(w’) < P_{m}(w)$
Nếu có, nghĩa là $m$ đã bị chia tay hoặc từ chối tỏ tình, có hai trường hợp xảy ra:
- Nếu $m$ đang hẹn hò với $w$, $w$ chia tay với $m$ vì tìm được mảnh ghép mình yêu thích hơn $m^{*}$, một cách hình thức $P_{w}(m^{*}) < P_{w}(m)$. Lưu ý là theo quan sát 1, chúng ta có thể thấy $P_{w}(m’) \le P_{w}(m^{*})$ (vẫn có khả năng $m^{*}$ là người cuối cùng hay nói cách khác $m^{*}$ là $m’$) suy ra $P_{w}(m’) < P_{w}(m)$.
- Nếu $m$ tỏ tình với $w$ nhưng bị từ chối, nghĩa là người yêu hiện tại của $w$ được yêu thích hơn $m^{**}$, một cách hình thức $P_{w}(m^{**}) < P_{w}(m)$. Lưu ý là theo quan sát 2, chúng ta có thể thấy $P_{w}(m’) \le P_{w}(m^{**})$ (vẫn có khả năng $m^{**}$ là người cuối cùng hay nói cách khác $m^{**}$ là $m’$) suy ra $P_{w}(m’) < P_{w}(m)$.
Thấy rõ chân trị của $P_{m}(w) < P_{m}(w’) \land P_{w}(m) < P_{w}(m’) $ luôn là một hằng sai. Nghĩa là giả sử ban đầu không bao giờ xảy ra. Suy ra không tồn tại hai cặp hôn nhân không bền vững có nguy cơ rạn nứt.
Từ đó suy ra $S$ là tập ghép bền vững.
Kết quả của thuật toán chấp nhận trì hoãn luôn đảm bảo hôn nhân bền vững!
3.2 Phân tích độ phức tạp thuật toán
Thuật toán chấp nhận trì hoãn có độ phức tạp $O(n^2)$, nhìn chung thuật toán lặp không quá $n^2$ vòng lặp tỏ tình, chi phí tính toán cho mỗi lần tỏ tình có thể thực hiện với độ phức tạp hằng số $O(1)$ (với điều kiện là hàm $P$ thiết kế hợp lí, tránh tính toán trong vòng lặp, chúng ta có thể tạo một mảng hai chiều $\mathtt{ranking}$ để làm việc này).
4. Cài đặt thuật toán
Thuật toán được ThetaLog cài đặt trên Python và Java, để tối ưu hóa việc cài đặt chúng ta nên lưu một mảng hai chiều $\mathtt{ranking}$ thay vì lập trình một hàm $P$ duyệt trên từng danh sách yêu thích để so sánh trong lúc chạy, lúc này tác vụ so sánh thứ hạng yêu thích sẽ là hằng số. Để đánh dấu $m$ đã tỏ tình với ai chúng ta có thể lưu danh sách yêu thích của $m$ dưới dạng cấu trúc dữ liệu động (Dynamic Data Structure) mỗi lần duyệt sẽ rút $w$ ra khỏi danh sách hoặc cấu trúc dữ liệu tỉnh (Static Data Structure) thì cần lưu thêm một mảng tạm để đánh dấu thứ tự duyệt.
Nếu dùng Python, đồng thời bạn muốn tìm hiểu các biến thể của thuật toán này trong kinh tế định lượng, Collection of variations on the Gale-Shapley Deffered Acceptance Algorithm có thể là những gì bạn cần tìm, phần cài đặt thuật toán được mô tả trong MatchingMarkets (algorithms/DA.py) của QuantEcon một thư viện mã nguồn mở mô hình kinh tế định lượng mới nổi gần đây.
# _______________________________________________________________________
# |[] ThetaLogShell |X]|!"|
# |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
# | > ThetaLog.com | |
# | > ENV: Python 3.6.5 Anaconda | |
# | > Deferred-Acceptance Algorithm | |
# |_____________________________________________________________________|/
def deferred_acceptance_algorithm(man_pref, woman_pref, n):
"""
Thuật toán chấp nhận trì hoãn (Gale-Shapley Algorithm)
# LƯU Ý: thuật toán cài đặt ở mã nguồn này đánh index từ 0
:param man_pref: list(list) - danh sách yêu thích của m thứ i là man_pref[i]
:param woman_pref: list(list) - danh sách yêu thích của w thứ i là woman_pref[i]
:param n: int - số lượng cặp đôi
:return stable_marriage: list(tuple) - mỗi một tuple(m, w) là một cặp hôn nhân
"""
# Người mà hiện tại w đang hẹn hò fall_in_love[w] = m
# Nếu đang trong độc thân fall_in_love[w] = -1
fall_in_love = [-1] * n
# Những người đàn ông độc thân
free_man = list(range(n))
# Hàm P: lưu thứ hạng w thích m rank[w][m]
ranking = [[0] * n for i in range(n)]
for i in range(n):
for j in range(n):
ranking[i][woman_pref[i][j]] = j
# chiến thuật tỏ tình bắt đầu
while free_man:
# xét một m độc thân
m = free_man[0]
# tỏ tình w mà hiện tại m thích nhất (không trả lại danh sách)
w = man_pref[m].pop(0)
# nếu w chưa hẹn hò
if fall_in_love[w] == -1:
# hẹn hò cùng m, m không còn độc thân
fall_in_love[w] = m
free_man.pop(0)
else:
# nếu w thích m hơn m'
if ranking[w][m] < ranking[w][fall_in_love[w]]:
# m hết độc thân, m' độc thân
free_man.pop(0)
free_man.append(fall_in_love[w])
# m và w hẹn hò
fall_in_love[w] = m
# Danh sách [(m,w),...] hôn nhân bền vững
stable_marriage = [(fall_in_love[i], i) for i in range(n)]
# trả về tập hôn nhân bền vững
return stable_marriagen = 4
man_pref = [[1,0,2,3],
[3,0,1,2],
[0,2,1,3],
[1,2,0,3]]
woman_pref = [[0,2,1,3],
[2,3,0,1],
[3,1,2,0],
[2,1,0,3]]
result = deferred_acceptance_algorithm(man_pref, woman_pref, n)
print(result)// _______________________________________________________________________
// |[] ThetaLogShell |X]|!"|
// |"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""|"|
// | > ThetaLog.com | |
// | > ENV: Java 1.8.0_181 | |
// | > Deferred-Acceptance Algorithm | |
// |_____________________________________________________________________|/
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class DemoDeferredAcceptanceAlgo {
public static int[][] deferredAcceptanceAlgo(int[][] manPref, int[][] womanPref, int n) {
// Danh sách những người m độc thân
Queue<Integer> freeMan = new LinkedList<>();
// Người mà hiện tại w đang hẹn hò fallInLove[w] = m
// Nếu đang trong độc thân fallInLove[w] = -1
int[] fallInLove = new int[n];
int[][] ranking = new int[n][n];
// Một mảng lưu tạm vị trí đang duyệt danh sách yêu thích của m
int[] next = new int[n];
// Khởi tạo tất cả độc thân
Arrays.fill(fallInLove, -1);
// Vị trí duyệt bằng 0 danh sách yêu thích m
Arrays.fill(next, 0);
// Lưu P dưới dạng mảng hai chiều Rạnking
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
ranking[i][womanPref[i][j]] = j;
}
}
// Tất cả m độc thân
for (int i = 0; i < n; i++) {
freeMan.add(i);
}
// Biến tạm
int m, w;
// chiến thuật tỏ tình bắt đầu
while (!freeMan.isEmpty()) {
// Xét m độc thân, chọn w yêu thích nhất chưa tỏ tình
m = freeMan.peek().intValue();
w = manPref[m][next[m]++];
// Nếu w đang độc thân
if (fallInLove[w] == -1) {
// m và w hẹn hò
fallInLove[w] = m;
freeMan.poll();
} else {
// nếu w thích m hơn m'
if (ranking[w][m] < ranking[w][fallInLove[m]]) {
// chia tay với m' và hẹn hò cùng m
freeMan.poll();
freeMan.add(fallInLove[w]);
fallInLove[w] = m;
}
}
}
int[][] stableMarriage = new int[n][2];
for (int i = 0; i < n; i++) {
stableMarriage[i][0] = fallInLove[i];
stableMarriage[i][1] = i;
}
// Trả về kết quả hôn nhân bền vững
return stableMarriage;
}
public static void main(String[] args) {
int n = 4;
int[][] manPref = {
{1, 0, 2, 3},
{3, 0, 1, 2},
{0, 2, 1, 3},
{1, 2, 0, 3}
};
int[][] womanPref = {
{0, 2, 1, 3},
{2, 3, 0, 1},
{3, 1, 2, 0},
{2, 1, 0, 3}
};
int[][] result = deferredAcceptanceAlgo(manPref, womanPref, n);
// In ra màn hình kết quả thuật toán
System.out.println(Arrays.deepToString(result));
}
}
5. Ứng dụng thuật toán
Thuật toán này được ứng dụng rộng rãi trong rất nhiều lĩnh vực: y tế, giáo dục, viễn thông, kinh tế,…
Đặc biệt trong kinh tế, Alvin Roth cho rằng các nghiên cứu lý thuyết của Gale-Shapley có thể làm sáng tỏ hoạt động của thị trường. Alvin Roth và cộng sự đã chứng minh ổn định là chìa khóa để hiểu rõ sự thành công của một thể chế thị trường nhất định. Sự cống hiến về lý thuyết của Gale, Shapley đồng hành cũng nổ lực nghiên cứu thực nghiệm của Roth đã mang đến giải Nobel kinh tế học 2012.
Một số ứng dụng tiêu biểu như sau:
- National Resident Matching Program
- How Game Theory Helped Improve New York City’s High School Application Process
- Thậm chí cả những ứng dụng liên quan đến mạng máy tính để ghép hàng tỷ người dùng và máy chủ, câu chuyện của Akamai: Algorithmic nuggets in content delivery
- Hiện tại, thuật toán này cũng vừa mới được ứng dụng vào nền giáo dục Việt Nam.
Thuật toán ứng dụng vào thực tế sẽ gặp nhiều khó khăn hơn, bạn đọc có thể tìm hiểu thêm các biến thể thuật toán ở nghiên cứu A survey of the stable marriage problem and its variants.
6. Phần kết
Thuật toán chấp nhận trì hoãn là một thuật toán giúp giải quyết bài toán hôn nhân bền vững. Kết quả trả về của thuật toán luôn luôn là một tập ghép bền vững. Thuật toán và các biến thể của nó ứng dụng rộng rãi vào nhiều bài toán thực tiễn: kinh tế, giáo dục, y tế, viễn thông,…
Tham khảo
- Prof. Vu Ha Van. Lấy người mình yêu và… không bỏ được (Nobel kinh tế 2012). Tháng Mười Một 13, 2012. https://vuhavan.wordpress.com/2012/11/13/lay-nguoi-minh-yeu-va-khong-bo-duoc-nobel-kinh-te-2012/
- Jon Kleinberg, Éva Tardos. Algorithm Design. http://www.cs.princeton.edu/~wayne/kleinberg-tardos/
- Blog Toán Học Cho Mọi Người - blogm4e. Vài nét về bài toán hôn nhân bền vững. https://blogm4e.wordpress.com/2016/09/09/vai-net-ve-bai-toan-hon-nhan-ben-vung/
- Prof. Vu Ha Van. VIASM, Mini-course: The Stable Marriage Problem. Feb 17, 2016. https://www.youtube.com/watch?v=9_mF1MxlHfk&list=PLukmhjLVAESnzsKNsiIT736qgYaOPt18P&index=1
- Blog Học Thế Nào. Về việc áp dụng thuật toán DAA của Gale-Shapley trong xét tuyển – Đối Thoại Giáo Dục. https://hocthenao.vn/2015/09/16/ve-viec-ap-dung-thuat-toan-daa-cua-gale-shapley-trong-xet-tuyen-doi-thoai-giao-duc/
- Wikipedia contributors. “Stable marriage problem.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 24 Sep. 2018. Web. 11 Oct. 2018.
- Vnexpress. Nobel Kinh tế 2012 thuộc về hai người Mỹ. https://kinhdoanh.vnexpress.net/tin-tuc/quoc-te/nobel-kinh-te-2012-thuoc-ve-hai-nguoi-my-2723231.html